aPARADOXON, a természettudomány ideiglenes kudarcai

Aparadox  15 A

    E=mc²  1905

A címben szereplő E=mc² a tudomány talán legfontosabb, de bizton a leghíresebb egyenlete. Az ifjú Einstein 1905 szeptemberében küldte el az erre vonatkozó kéziratát az Anallen der Physics német folyóiratnak. Manapság ehhez a dátumhoz kötik mind a téma felvetését, mind a megoldását. 

  Ezzel szemben nagytekintélyű fizikusok, mint Lorentz és Langevin évekkel Einstein előtt kifejtették a tömeg és energia kapcsolatát, lényegében az E=mc² képletet. Talán csak elvi jelentőségűnek tűnik, de a 2 hatványkitevő helyett kicsit kisebbre, kb. 1,98-ra voksoltak. Más helyen látni fogjuk, hogy a kissé furcsa szám nem volt teljesen alaptalan.

 Amikor Einstein nekiállt elméleti dolgozata megírásának, akkor már nem vakrepülést végzett. A merész ötlet, az anyagban szunnyadó energia gondolata már létezett. Továbbá ajánlatosnak tűnt számára a nagyok számszerű eredményeit tisztelni, azaz egy mc^1,98 körüli képletet megcélozni. Gondolhatott volna arra is, hogy a mozgási energia ismert képletét kellene eredményül kapnia, azaz az E=mv²/2 képletet.  Fénysugár esetében ez nyilván az E=mc²/2 alakot öltené. De itt leginkább az E=mc² eredmény körüli érték tűnt kecsegtetőnek.  Ezért hát nekiállt, hogy kicsivel korábban megírt relativitáselméletéből ezt a képletet vezesse le. 

  Az 1906-ban napvilágot látott dolgozatot nem könnyű követni. Ezért segítési céllal az alábbiakban néhány megjegyzést szeretnék előrebocsátani. 

●  Einstein egy olyan testről beszél, amely áll az űrben, és közben „sugároz”. Feltehetőleg fényt sugároz.  A kikötés szerint kizárólag előre és hátra, azonos intenzitással.

●  Einstein  behelyez két koordinátarendszert is az űrbe. Egyiket a sugárzó test mellé, míg a másikat csak úgy, egy kicsivel arrébb.  Tegyünk ez utóbbiba egy második sugárzó testet, mert igen rosszul viselem az absztrakt koordinátákat valódi testek nélkül.

    Mindezek után két izzó sziklát kezdünk látni a sötét űrben. Csakhogy a valódi  izzó sziklák nem előre-hátra, hanem körbe-körbe sugároznak! Engem a cikk olvasása közben folytonosan irritált e két furcsa szikla, amely kizárólag két szűk sávban sugároz. Pedig megszokhattam volna, hogy Einstein mindig életidegen és csontvázra kopaszított, ezért többértelmű példákat kreál.  Kellő számú, és a hagyományos menetbe jól illeszkedő foggantyúk hiányában a példáiból bármi következhet, vagy akár annak ellenkezője is. 

●   A sziklák helyett javaslok két autót, melyeknek mind az elülső reflektora, mind a tolatólámpája világít. Így a fénysugarak impulzusa kiegyenlített. 

●  A levezetés szerint az 1. számú autó és az (x,y,z) koordinátarendszer áll.  A 2. számú autó (és benne egy megfigyelő) v sebességgel mozog a (x,h,z) koordinátarendszerrel együtt. A mozgás iránya az x és a x tengellyel párhuzamos. 

   Vélhetőleg van egy 3. teljesen független megfigyelő is egy szintén álló (x',y’,z') koordinátarendszerben. Legyen ez maga Einstein, egy fix pont az ő „minden-mozog’’ világában. Ő tehát állónak látja az 1. autót, és mozgónak a 2. autót. 

●  Az 1. számú autó reflektora a levezetés szerint nem vízszintesen van beállítva, hanem j (fi) szöget zár be az x tengellyel. Einstein ezzel nyilván az általános megoldás illúzióját kívánta kelteni, miközben az általános térbeli megoldáshoz 3 térszög (j_x, j_y,j_z) tartozik. 

   A levezetés kétségbeejtően sok (11) jelölést használ el a test energiájára. Kezdjünk megbarátkozni velük!  Íme:

l   l*  L/2  L  E1  H1  E0  H0   K0   K1  C

●  Nyilvánvaló, hogy a levezetés igényli az ábrát, melyet Einstein szokása szerint elmulasztott elkészíteni. Pótolom a mulasztását, bár a szöveg alapján elég bizonytalan e rekonstrukciós művelet. (Aki jobbat tud rajzolni, tegye közzé!)

 Meglehet, hogy kevesen tudják, de a kis Albert kiskamasz korában igen magas szintet ért el a síkgeometria terén. Elolvasott egy kiemelkedően jó ismeretterjesztő könyvet, majd felcsigázott érdeklődéssel vette kezébe a vaskos hivatalos Geometria könyvet. Ezt azonban mint színvonaltalant hamarosan sutba dobta. Kívülálló számára szinte érthetetlen, hogy 26 éves korára miként sikerült leküzdenie magát a nulla színvonal alá.

●  Mindezek előrebocsátása után következzék a híres dolgozat! Akár műveltségi minimumnak is tekinthetjük ennek végigolvasását.  Kiváltképpen vonatkozik ez azokra, akik hivatkozni is szoktak az E=mc² képletre, mint az emberiség kimagasló szellemi teljesítményére.  Ámbár nehéz olvasmány lesz, tekinthetjük egyféle penitenciának. Végül is mindenkinek vannak kisebb-nagyobb bűnei, sőt még itt van az un. eredendő bűn is.  Tapasztalni fogjuk, hogy a figyelmes cikkolvasás felér egy komoly vezekléssel.

Albert Einstein: 

Függ-e a test tehetetlensége energiatartalmától?

(1905)

A jelen folyóiratban általam nemrégiben közölt elektrodinamikai vizsgálat eredményeinek egy igen érdekes következményük van, amelyet a következőkben le akarok vezetni.

Előző cikkemben a légüres térre vonatkozó Maxwell- Hertz egyenleteket, a tér elektromágneses energiájára vonatkozó Maxwell­-féle képletet, továbbá az alábbi elvet vettem kiindulási alapul:

Azok a törvények, amelyek szerint a fizikai rendszerek állapota változik, függetlenek attól, hogy egymáshoz képest egyenes vona­lú egyenletes mozgást végző két koordináta-rendszer közül melyikre vonatkoztatjuk az állapotváltozást (relativitáselv).

Ezekre az alapokra támaszkodva egyebek között az alábbi ered­ményt vezettem le (id. mű, 8. szakasz):

Sík fényhullámok egy rendszerének legyen az (x, y, z) koordiná­ta-rendszerre vonatkoztatott energiája l; a sugárirány (hullám normális) alkosson j szöget a rendszer x-tengelyével. Ha új, az (x, y, z) rend­szerhez képest egyenes vonalú egyenletes mozgást végző (x, h, z) koordináta-rendszert vezetünk be, amelynek kezdőpontja v sebes­séggel mozog az x tengely mentén, a kérdéses fénymennyiségnek – a (x, h, z) rendszerben mért – l^* energiája a következő:

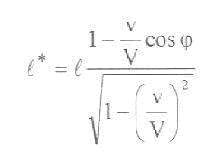
ahol V a fénysebesség. A következőkben ezt az eredményt használ­juk majd fel.

Legyen most az (x, y, z) rendszerben egy nyugvó állapotú test, amelynek energiája – az (x, y, z) rendszerre vonatkoztatva – legyen E₀. Az ehhez képest v sebességgel mozgó ((x, h, z)  rendszerben le­gyen a test energiája H₀.

A test bocsásson ki az x-tengellyel j szöget alkotó, L/2 energiájú (az (x, y, z) rendszerben mérve) sík fényhullámot, s ezzel egyidejű­leg az ellentétes irányba is bocsásson ki ugyanakkora fénymennyi­séget. A test eközben az (x, y, z) rendszerre vonatkoztatva nyuga­lomban marad. A jelenségre érvényes az energiaelv, mégpedig (a relativitáselv szerint) mindkét koordináta-rendszerre vonatkoztatva. Legyen a test energiája a fénykibocsátás után az (x, y, z), illetve (x, h, z) rendszerben mérve, E₁, illetve H₁. A fentebb közölt összefüg­gés szerint ekkor:

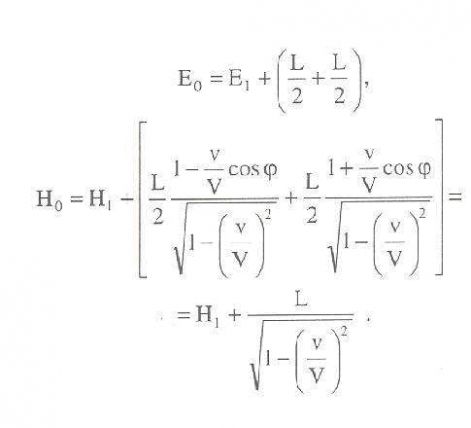
Ezekből az egyenletekből kivonással ezt kapjuk:

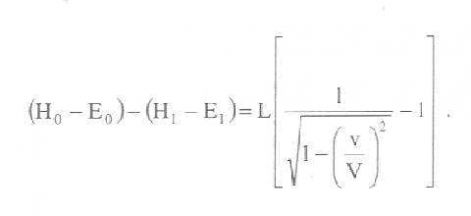
A kifejezésben szereplő két, (H – E) alakú különbségnek egyszerű fizikai jelentése van. H és E ugyanannak a testnek két különböző, egy­máshoz képest mozgó koordináta-rendszerbeli energiája, ha a test az egyik rendszerben (az [x, y, z] rendszerben) nyugalomban van. Vilá­gos tehát, hogy a H – E különbség a test K mozgási energiájától a másik rendszerhez (a [(x, h, z] rendszerhez) képest csupán a C additív állandóban különbözhet, amely a H és E energiák önkényes additív állandóinak a megválasztásától függ. Felírhatjuk tehát:

H₀ - E₀ = K₀+ C

H₁- E₁- K₁+ C

minthogy C a fénykibocsátás közben nem változik. Ezt kapjuk te­hát

:

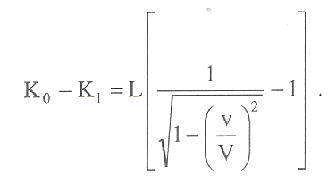
A testnek ((x, h, z) rendszerre vonatkozó mozgási energiája a fénykibocsátás következtében csökken, mégpedig a testek anyagi minőségétől független mértékben. A K₀-K₁ különbség továbbá ugyanúgy függ a sebességtől, mint az elektron mozgási energiája (id. mű, 10. szakasz).A negyed- és magasabb rendű mennyiségek elhanyagolásával felírhatjuk:

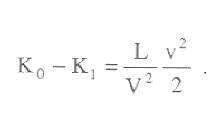
Ebből az egyenletből közvetlenül következik:

Ha egy test sugárzás alakjában L energiát ad le, tömege L/V²-tel csökken. Nyilvánvalóan lényegtelen, hogy a testtől elvett energia éppen sugárzási energiává alakul, úgyhogy az alábbi általánosabb következtetésre jutunk:

A testek tömege energiatartalmuknak a mértéke; ha az energiá­juk L-lel változik, tömegük ugyanolyan értelemben L/9 · 10²⁰-nal vál­tozik, ha az energiát ergben, a tömeget pedig grammban mérjük.

Nem kizárt eset, hogy olyan testeken, amelyek energiatartalma nagymértékben változó (például a rádium sókon) sikerül majd az elmélet helyességét bebizonyítani.

Ha az elmélet egyezik a tényekkel, a sugárzás a fényt kibocsátó és elnyelő testek között tehetetlenséget visz át.

(Albert Einstein: Válogatott tanulmányok,

Gondolat, Budapest, 1971., 74-77. oldal.)

Most az Einstein tanulmány után egy jóval érthetőbb rész következik, Murguly György szakíró elemző gondolatai.  Az idő nem múlik c. könyvéből illesztettem ide néhány bekezdést.  A Szerző könyve döntően a tér, az idő és a végtelen kapcsolatát tárgyalja, de szerencsére szakít néhány oldalt (321 – 340 oldal) az ominózus dolgozat belső ellentmondásaira és a valódi fizikai háttér feltárására.  Íme a részletek: 

■    Mindjárt az elsőként bemutatott képletből és az azt bevezető magyarázatból kitűnik, hogy a Lorentz-transzformáció l* és l energiára értelmezett részösszefüggéséről van szó, amelyben az együttható a közvetlen átszámítási tényező. Az eltérést mindössze a számlálóban lévő kifejezés (1 - v/V cos(j) ) jelenti, ami, az 1et kivéve, a levezetés során egyébként is kiesik.

 ■     Ha az E=mc² levezetésének – merthogy arról van szó – ez a képletekbe foglalt összefüggés az induló feltétele, akkor érthetőek a végeredményt illető kétségeink. Ez idáig ugyanis már sokszorosan bebizonyosodott, hogy a Lorentz-transzformációnak semmi köze azokhoz a jelenségekhez, amelyekre azt A. Einstein megpróbálta alkalmazni.

 ■     Feltehető a kérdés, hogy miért éppen L/2 a kibocsátott fényenergia mennyisége?

       A test helyben maradna akkor is, ha mindkét irányban L energia lenne kibocsátva. A választ a levezetésben találjuk meg. A felhasznált képlet számlálójában szereplő -v/V cos(j) csak úgy ejthető ki, ha levezetés közben hozzáadjuk a +v/V cos(j) összefüggést, mint az általa ugyanúgy meghatározott, másik irányba kibocsátott fénymennyiséget. A kétszer L/2-re a levezetés első képletében így azért volt szükség, hogy a kiejtések után az összefüggésben csak egy (egy darab) L maradjon, mert a levezetés végén nem felelt volna meg a már előre kifundált elvárásoknak.

 ■  Ezek a műfeltételek az utolsó előtti egyenlet alakjában és összefüggéseiben realizálódtak, ahol az induló feltételekhez képest – mint látható – a lényeget tekintve gyakorlatilag semmi nem változott az utolsó lépés megtétele előtt, mert továbbra is a Lorentz-transzformáció együtthatója a meghatározó.

 ■     Az L a test által kibocsátott fénymennyiségnek azt az energiáját jelenti, ami a test mozgó rendszerhez viszonyított energiájának K₀ - K₁ csökkenését okozza. A V a fénysebességet, v pedig a fénymennyiséget kibocsátó testhez képest mozgó koordináta-rendszer sebességét jelenti.

 ■    Nem a test mozog tehát, hanem a hozzá viszonyított koordináta-rendszer, amelyből a mozdulatlan test mozgási energiája veszteségének a „mérése" történik. Annak a mérése, ami a testnek nem is volt, hiszen az mozdulatlan. A mozgó rendszerre és erre a fordított alapállásra az együttható bevezethetősége miatt volt szükség. A végeredmény ugyanis (az L kivételével) ebből lett „kihozva".

 ■     A feltárt logikai hézagot követően a kívánt végeredmény csak ez által válik lehetségessé, ami az alakjára nézve tökéletesen megfelelő, miközben az eredeti összefüggésekhez semmi köze.

—     O O O   —

Az Einstein dolgozat analíziseként már csak egy problémát kívánok megemlíteni. „Nyilvánvalóan lényegtelen, hogy a testtől elvett energia éppen sugárzási energiává alakul, úgyhogy az alábbi általánosabb következtetésre jutunk. stb.” – veti oda könnyedén Einstein. Egyáltalán nem nyilvánvaló, hogy a fénysugárból levont következtetések a közönséges anyagra is vonatkoznak. A mai fizika szerint a fénynek (fotonnak) nincs is tömege, tehát nem anyag. Azaz Einstein következtetése ez esetben is egy felelőtlen extrapoláció. Megemlítem, hogy az E=mc² 2013 dolgozatomban a fény és az energia közötti kapcsolatot viszonylag problémamentesen sikerül levezetnem, míg az anyagra vonatkozót csak jelentős nehézségek árán.