Tassi Tamás

 

 

 

A hatáskvantum csapdájában

 

 

azaz

in the trap of the planck-constant

 

              A "modern" fizikáról klasszikusan és közérthetően.             

 

"Planck hosszú ideig próbálkozott azzal, hogy a hatáskvantumot beillessze a klasszikus fizika kereteibe. Tudjuk, hogy ez a törekvése nem sikerült, mert a mikrovilágban ettől merőben eltérő törvények érvényesülnek."

Professor emeritus Nagy Károly  ELTE

 

A h kvantumállandó, más néven Planck állandó, vagy megint más néven hatáskvantum lényegének közelébe leggyorsabban  a mértékegysége útján juthatunk el: kgm²/s. Ez azt mutatja, hogy ebben a furfangos fizikai állandóban az m tömeg, a v sebesség és egy r keringési sugár van összeszorozva: mvr.  Persze, a dolog nem ilyen egyszerű, de továbbhaladva - és néhány vargabetűt leírva - meg fogjuk érteni az igazi lényegét.  Erre azért érdemes időt és energiát áldozni, mert ezt az alapvető fontosságú fizikai fogalmat szinte senki sem  érti.  Aki meg azt hiszi, hogy érti, az félreérti.

 

 Az mvr szorzat szerepe igen jelentős a fizikában.  Impulzusmomentumnak, impulzusnyomatéknak vagy perdületnek nevezik, de esetenként hívják forgási-nyomatéknak vagy pálya-nyomatéknak is.  Ez utóbbi fogalomnak fontos szerepe van a csillagászatban, amennyiben a bolygók keringése során ez egy megbízhatóan megmaradó mennyiség. (Ellentétben a pályasugárral, a sebességgel valamint az impulzussal, mert ezek a keringés során folytonosan változnak.)

 

Perdület

 

Központi égitestünk a Nap.  Ez egy hatalmas gázgolyóbis, mely forog a saját tengelye körül. Perdülete óriási, azonban Földünk pálya-momentuma (perdülete) még ennél is 3000-szer nagyobb. Azért ilyen nagy, mert a Föld esetében a perdület mvr képletében nagy a  v sebesség és az r sugár értéke.  A 3 tagú szorzatban egy 30000 és egy 150 milliárd tag lesz a domináns.

  Talán kevésbé ismert, de az elemi részecskéknek is van perdülete, impulzusmomentuma. Ezt angol szóval spinnek mondják, és ez ugyanúgy egy megmaradó mennyiség. Van azonban néhány jelentős különbség az égitestek és az elemi részecskék impulzus-momentuma között. Az égitestek egyszerűen csak megtartották és mindmáig őrzik a keletkezésük időpontjában örökölt perdületet. Nem is tudnák egykönnyen  elveszíteni, hiszen az roppant nagy fizikai mennyiség.  Földünk esetében mintegy 2,7*10⁴⁰ kgm²/s. Ugyanakkor az elemi részecskék impulzus-nyomatéka jelentéktelen.  Legkisebb és egyben tipikus értéke 53*10^-36. Mintegy 75 nagyságrenddel kisebb, mint a Földünké. Valószínűtlen, hogy ez a pici érték évmilliárdokon keresztül megőrizhető. Inkább az a helyzet, hogy valami láthatatlan entitás rejtőzik a háttérben, és ez folyamatosan feltölti a részecske impulzus-momentumát az általa megszabott értékre.

 

Nap és Elektron

 

Most hasonlítsuk össze a Napot és az elemi részecskéket a perdület minősége szempontjából!  Az elemi részecske - tipikusan egy elektron -  nem képes saját belsejében elegendő perdületet tárolni. Ehhez túl kicsi a mérete.  Forgási sebesség tekintetében ugyanis át kellene lépnie a fizika korlátait, jelesül a fénysebességet. Marad számára az a változat, hogy nem a Napot próbálja leutánozni, azaz nem forog. Forgás helyett bolygó módjára kering, és ily módon nagy értékű pálya-momentumra tesz szert. A forgási középpont lehetne egy atommag, de akár a vákuum m₀ mágneses permeabilitása is körmozgásra kényszerítheti.

 

Max Planck

 

Mindezek után térjünk át a címben szereplő hatáskvantumra. A h hatáskvantum szülőhelye egy kívülről hevített üreg volt, amelyből csak egy kis lyukon jött ki a hőmérsékleti sugárzás.  Az üreg belsejét alkotó atomok energia szintjét átvették az össze-vissza pattogó fotonok. Mire kiértek, energia-eloszlásuk pontosan lekövette a belső jellemzőket, és egy un. haranggörbe-diagramm alakult ki.

 

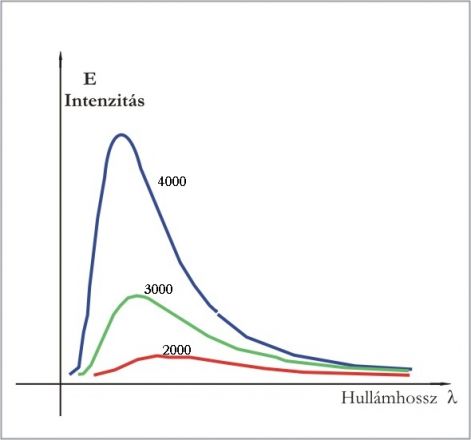
Az ábra 3 haranggörbét mutat. Minél magasabb az üreg hőmérséklete, annál magasabban halad a görbe. Az intenzitás-csúcsok pedig balra, a kisebb hullámhosszak és a nagyobb energiák felé tolódnak el. A vízszintes tengely beosztása nyílván nem lineális, mert  fele hullámhosszhoz kétszeres foton-energia tartozik. (Ez a skálázás a 0 hullámhossz környékén bizonyára meghaladja képzelőerőnk korlátait.)

 

 Egykor a fizikusok hosszan viaskodtak e görbék alakjával. Miért közelít a 0-hoz a kis hullámhosszakon (nagyenergiákon) valamint a nagy hullámhosszakon (a kis energiákon)? Most már tudjuk. Azért, mert a fotonok testvériesen, sőt igazságosan osztoznak az energián.  Az átlaghoz képest csak kevés fotonnak jut sok energia, és  kevés foton szűkölködik energiában.

 Maga a haranggörbe-eloszlás is egy hétköznapi dolog.  A szobánkban lévő levegő molekulái is ekképpen osztoznak a hőenergián. Az átlagsebesség cca 500 m/s, de  a véletlen ütközések folytán bőven vannak kisebb sebességű, és ezáltal kisebb mozgási energiájú molekulák. És persze vannak nagyobb sebességűek is. 

 Ennyi kitérő után térjünk vissza a címben szereplő hatáskvantumhoz.  Ezt a fizikai jellemzőt a fénysugarak vizsgálata közben fedezték fel. Leginkább a szubatomi részecskékre hat, valójában mégis a vákuum  egyik alapvető tulajdonsága.  Jele h , ami szerencsésen összecseng a magyar hatáskvantum szóval.  Szinte kínálja magát, hogy örökre tartsuk meg, miközben - mint látni fogjuk - jó lenne ezt a kiemelt fogalmat elfeledni. 

 A vákuumnak a h hatáskvantum mellett sok más fontos fizikai jellemzője is van. Ilyen az e₀ dielektromos állandó, a m₀ mágneses permeabilitás, a Z₀ hullámellenállás, valamint a c fénysebesség. Ez utóbbi tulajdonképpen nem is önálló fogalom, az előzőkből képezhető: c = (e₀*m₀)^-0,5. De ott van a listában főtémánk, a h hatáskvantum, a belőle képzett ћ (há-vonás), továbbá egy sűrűn emlegetett 1/2, ami a h/2p értéket takarja. Ez utóbbi furcsaságok helyett azonban célszerűbb lesz egy valódi vákuum-paramétert, az S₀ vákuum-perdületet bevezetni. Ez az évszázados vákuum-paraméterekhez hasonlóan közvetlenül nem észlelhető. Számszerű értéke viszont pontosan megegyezik az extrém elnevezésű spinnel, az 1/2-el. Leginkább a szubatomi részecskék világában jelentkezik, azok perdületét - angol szóval spinjét - adja meg. (Az állandók számszerű értékei a cikk végén lévő táblázatban láthatók.)

 

A Planck-formula

 

 

A h hatáskvantum erőssége a foton energia-képletében játszott főszerepe. Ezt a képletet megalkotójáról egy évszázad óta Planck-formulának nevezik:

  EPlanck = h*n    joule

Ami azt jelenti, hogy a h állandót a n (nű) frekvenciával szorozva megkapjuk az adott foton energiáját. Ez annyira szép és egyszerű, mint egy tündérmese. Ugyan ki szeretne ennél szebbet és egyszerűbbet? Ez a szépség elkápráztatta a tudósokat. Szemüket a fényesen tündöklő h betűre függesztve a hatáskvantum fénycsapdájának foglyaivá váltak. Hasonlóan ahhoz, ahogyan a lepkéket és bogarakat elvakítja és magához láncolja az erős fény. Valójában mindnyájan különböző csapdákban ülünk - szociális, pénzügyi, politikai, globalizációs, média stb. - megbűvölt és elvakított állapotban.  A hatáskvantum csapdája ezeknél jóval elegánsabb!

 

 

Amint később látni fogjuk, a képletnek nincs értelme, ámbár számszerűen jó eredményt ad. A Planck képlet elnagyolt képet ad a fotonok világáról, ezért részletezése reményt adna arra, hogy közelebb jussunk a h lényegéhez. Azonban energia-takarékosabb a  foton energiáját az S₀ vákuum-perdületből levezetni.

 

Perdületből energia!

 

Készítsünk gondolatban egy egyszerűsített fotont! Elhelyezünk egy pici m tömeget egy gyorsan forgó tárcsán, azaz a fotont síkbeli mozgásra kényszerítjük. Mint minden elemi részecske, kapjon ez is S₀=mvr=53*10^-36 értékű keringési impulzust. (Ez az érték nekünk kicsi, de egy fotonnak hatalmas.)

 

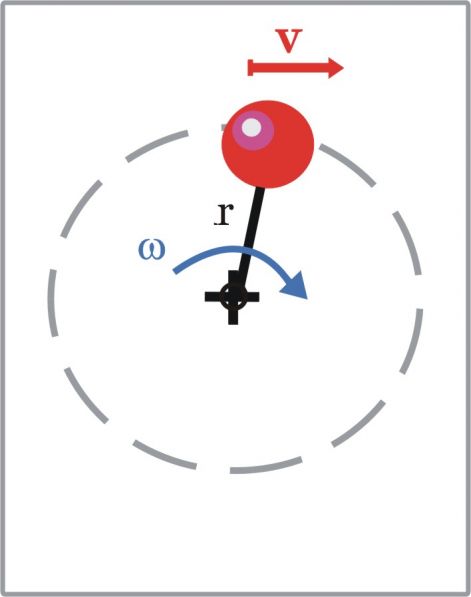
Legyen a másodpercenként megtett fordulatok száma - a  frekvencia -  n (nű).  Ekkor a mozgási energia:

E1m=p*S₀*n

 

 

 

 

 

 

Ezt hamar belátjuk, ha meggondoljuk, hogy a kerületi sebesség v=r*w(omega), ahol w=2p*n. Ezt az energia képletébe helyettesítve:

E1m = p*(mvr)*n = p*(m*v*2p*n)/2p = mv²/2.

Ez utóbbi pedig már a mozgási energia jól ismert képlete.

 

2 golyó a tárcsán

 

Első hallásra talán meglepő, de a tárcsára nem 1, hanem 2 darab m tömegű részecskét kell helyeznünk.

 

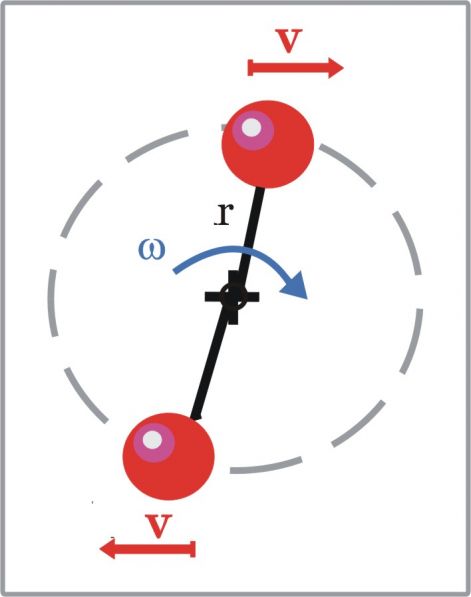
A foton a fizikai levezetésekben gyakorta mutat kettős tulajdonságot. De a legfőbb indok, hogy a fotonnak 2S₀ spinje van. A kettőzött spin miatt energiája is kétszeres lesz:

E2m = p*2S0*n

 

 

 

 

Térbeli csavarvonal

 

Ezidáig csak síkban foroghatott a foton, a forgó tárcsára rögzítve. Ha szabadjára engedjük, akkor a vákuum m0 mágneses permeabilitása különleges dolgot fog művelni. Az m tömegekre felfelé irányuló sebességet kényszerít, és ennek utána az m golyócskák térbeli kettős csavarvonal-pályát írnak le. Ha a sebességük a tárcsán c volt, akkor a felfelé-mozgás sebessége is c lesz.  Mindez a térben 1,41c sebességet jelent. Sajnos ebből mi csak a haladás c sebességét észleljük.

 

 A most előtűnt c haladási sebesség is mozgási energiát jelent. Ez természetesen azonos lesz a forgásból kapottal, hiszen a sebesség azonos: 

 

E_halad=2E_2m=p*2S₀*c

 

Most már felírhatjuk egy igazi foton energiáját, mint a keringés és a haladás energiájának összegét. Az alsó indexben lévő spin szó jelzi, hogy az energia a vákuum perdületéből, a spinből van levezetve:

 

   E_spin=p*2S₀*n+p*2S₀*n,

azaz összegezve:

 E_spin=4*pS₀*n     [joule]

 

Meredek csavarorsó

 

Képesek vagyunk arra, hogy a foton furcsa mozgását modellezzük egy technikai eszköz segítségével. Ez egy meredek emelkedésű csavarorsó.

 

 

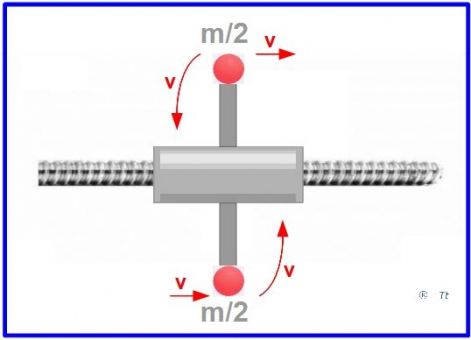Egy nagyméretű menetes anya forog rajta, és a forgásiránytól függően halad előre vagy hátra.  Képviselje tehetetlen tömegét a hengeres palástjára kihelyezett 2 darab m tömegpont. Ezek mindkét fő irányban v sebességgel rendelkeznek tengely-irányban is, és forgásirányban is. Mozgási energiájuk tehát irányonként 2m*v2/2. A két fő irányt összegezve tehát energiájuk 4mv2/2.

 

 Ha meggondoljuk, irányokra bontott energia a valóságban nem is létezik, hanem csak összenergia.  Más úton is megkaphatjuk az összenergiát, mert rendelkezésünkre áll az 1,41 v összegzett térbeli sebesség.  Az így felírt mozgási energia képlete az első pillanatban talán bonyolultnak tűnik, de a végén majd visszajutunk a fent levezetett képlethez:

 

E_2m=2m*(1,41v)²/2=2m*2v²/2=4*mv²/2

 

Ugyancsak duplázódik a forgó henger lendülete, impulzusa is. Ha távolról szemléljük a szerkezetet, akkor nem látjuk a sima hengerpalást forgását.  Azt látjuk, hogy egy henger halad a rúd egyik végétől a másik végéig.  Akkor fogunk meglepődni, ha odaállunk a végéhez és  próbáljuk megállítani a hengert. Kétszeres erővel fog hátralökni bennünket, mint amire számítottunk. Persze, hiszen a forgás energiája is átalakul előre mutató impulzussá. A kettős mozgás miatt ennek a szerkezetnek kétszeres energiája és kétszeres impulzusa van.  A kiinduláskor felvett 2m tömeg következtében pedig 4-szeres.  Csakúgy, mint a foton esetében. 

 

A foton

A fentiekben már láttunk néhány utalást arra, hogyan is kell kinéznie egy fotonnak.  Két pici tömeg kering egymás körül, és közben előre haladnak.

 

  

A tömegek 0-nál nagyobbak, de tipikus esetben sok nagyságrenddel kisebbek egy elektron-pozitron párnál.  Elektromos vonzás nem is szükséges a kapcsolódáshoz. Ismert a szupravezető esete, ahol két taszító elektron áll össze szoros párrá.  A foton tömege vélhetőleg nem a semmiből keletkezik, hanem például a vákuumban lévő virtuális elektron-pozitron párból.  Egy legerjedő atom kelti életre, és indítja útjára.  Becsapódáskor a tömeg pár leadja energiáját és újra beleolvad a háttérbe.  Azonban minden ellenkező híreszteléssel szemben a foton haladása közben rendelkezik tömeggel, impulzussal és energiával.  A frekvencia ismeretében ez utóbbit már kétféle képlettel is kiszámíthatjuk, ahol  a két számítás egyazon eredményt ad:

EPlanck = h*n   és

Espin = 4p*S0*n

Vegyük észre, hogy az EPlanck egy alacsony szintű tapasztalati képlet, a h pedig mindössze egy tapasztalati állandó.  Ezzel szemben az Espin levezetett képlet, ami több fizikai tényező között teremt kapcsolatot.   

 

Mi is a hatáskvantum?

A fenti két képlet láttán gond nélkül fel tudjuk írni a h hatáskvantum egyenletét:

h = 4p*S₀

Itt a 4p a vákuum-perdület szorzója, értéke 12,56. Ha ez a szám 11 lenne, akkor sokan ismerősnek vélnék.  Akkor ez egy focicsapat, és - főleg a férfiak - azonnal felismernék a logikát a zöld gyepen futkározó játékosok látszólag rendszertelen mozgásában. A h hatáskvantum 12,56 szorzója kevésbé logikus és kevésbé felismerhető. Ellenben fentebb áttekintettük a logikus utat, hogyan lehet a foton energiáját az S₀-ból származtatni. (A levezetés jóval rövidebb is lehetne, ha nem egy nagy halom téveszme alól kellene előhuzigálni az esszenciát.)

 

Joule-szekundum?

 

A fizikusok közel évszázados próbálkozása volt, hogy megpróbálják a h állandót a mértékegysége alapján értelmezni. A munka definíciója: Erő szorozva a megtett úttal. Mértékegységben gondolkodva newton*méter, azaz kgm/s2*m. A munka mértékegysége tehát kgm²/s². Ezzel szemben a h képlete definíció szerint h=mvr. Mértékegységet nézve kg*m/s*m, azaz kgm²/s,  azaz Js. Némi bővítés árán a kgm²/s-ből Js-t készítettek, ami azt mondja, hogy ez munka, az időtartam hosszával szorozva. Ezt a nem létező időtartamot-toldalékot  elnevezték hatásnak, a kvantumos h-t pedig hatáskvantumnak.

 

   Amint azt a bevezetőben említettük, Planck hosszú ideig próbálkozott azzal, hogy a hatáskvantumot beillessze a klasszikus fizika kereteibe. Íme, most bent van! Planck így is megtette a magáét, jogos tehát a centenáriumra írt elismerő megemlékezés Nagy professzor részéről. Ugyanakkor hiba volt a kiút keresését feladni, és végleg elismerni az emberi logika kudarcát a szellem-kvantumokkal vívott csatában. Ez egy rendkívüli fontosságú csata, ezt soha sem szabad feladni, tehát muszáj nyerni. De nem elég nyerni, azt el is kell hinni! Közel 1 éve fekteti el néhány fizikaprofesszor ezt a klasszikus gondolatmenetet követő dolgozatot. Az ódzkodásnak sok oka van. Csak az egyik, hogy ők, a hivatásos fizikusok lélekben nemcsak az ütközeteket, hanem a háborút is elvesztették. Mára már a h hatáskvantum béke diktátumát megalkuvással és csöndes beletörődéssel elfogadták.

 

 

2012 június hó

Tassi Tamás 

 

E cikk eredetijének nyomtatható változata A4-es jpg formában elérhető a következő helyen:

              

               1. oldal                        2. oldal                           3. oldal

 

  <<  Vissza                                           Tovább  >>  

                 ELTE az első 500-ban                                          Atomok aurája

 

 A téma feldolgozása más formában:

  

     Foton és hatáskvantum  lásd itt!

 

 

Lektorálva : 2019 május 14.

 

Kulcsszavak: Einstein, cézium, atomóra, Hafele, Keating, kísérlet, Kelly, atommag, proton, neutron, gluon, h hatáskvantum, Planck-állandó, vákuum, foton, Einstein, relatív sebesség,

 A legfrissebb cikk:

 

 

7  új magyar Nobel-díj esély

Read more: http://aparadox.hupont.hu/1#ixzz2W1KpOoMM

Oldal: A hatáskvantum csapdájában
aPARADOXON, a természettudomány ideiglenes kudarcai - © 2008 - 2024 - aparadox.hupont.hu

Az, hogy weboldal ingyen annyit jelent, hogy minden ingyenes és korlátlan: weboldal ingyen.

ÁSZF | Adatvédelmi Nyilatkozat