Anyagból energia: E=mc²  2013

 

 

A világhírű E=mc² egyenlet az Annalen der Physik tudományos folyóiratban jelent meg 1906-ban. Ámde több hibát is hordoz magában.  Hibás a kiinduló alap, a jelölések rendszere, a levezetés logikája stb. Furcsa módon azonban a végeredmény az jó. Mivel a tudomány mindezideig nem korrigált, ezért kívűlállóként  magam végeztem el a problémás dolgozat újragondolását. Két különböző területre is levezettem a képletet, és ezek a levezetések az alábbiakban láthatók. 

 

Vegyünk fel egy követ a földről, és sétáljunk vele! Azt tanultuk, hogy ilyenkor a kőnek helyzeti és mozgási energiája van. Esetleg még azt is ki tudnánk számolni, hogy számszerűen mennyi.  Most ejtsük el a követ. Triviálisnak tűnik, hogy helyzeti és mozgási energiáját elveszítette, így most már energiatartalma ismét nulla. 

 A fizikusok 1900 táján döbbentek rá, hogy az elheverő kőnek is van energiája – rejtőző energiája – mégpedig felfoghatatlanul nagy. Az 1 kilogrammos kőben 90 000 000 000 000 000 joule energia rejtőzik. Az anyag tárolja magában ezt az iszonyú mennyiségű energiát, szerves része a kőnek. Nagy szerencsénk van, hogy egy csöpp sem szivárog belőle, mert ekkora mennyiségből a leg csekélyebb is túl sok lenne. 

 Gondolkodjunk el azon, hogy miből is van a kő? Egy törpe kisebbség azt vallja, hogy anyagcsírákból és energiából. Jómagam is e kisebbséghez tartozom, aki nélkülözhetetlennek tart némi pro-anyagot, melyet azután az energia fúj fel „valódi”  anyaggá, esetünkben kővé. A háziasszony először kis tésztakorongokat helyez a tepsibe, majd beteszi a forró sütőbe. A sütő hőenergiája ezek méretét megnöveli, és finom pogácsává varázsolja.  Ámde logikai tévúton jár az, aki elhiszi, hogy lehet pogácsát készíteni kizárólag csak forróságból!

 Manapság már egyetértés van abban, miszerint az anyagban rengeteg sok rejtett energia van. Anno számos jeles fizikus jutott arra a gondolatra, hogy ez az energia a tömeggel és a fénysebesség valamely hatványával arányos. A gyorsan mozgó testek tömegnövekedését Kaufmann észlelte kísérletileg 1901-ben, majd ugyanerre Pais és Lorentz adott képletet. Lorentz és Langevin évekkel Einstein előtt kifejtette a tömeg és energia kapcsolatát, lényegében az E=mc² képletet. Talán csak elvi jelentőségűnek tűnik, de mégis fontos, hogy a 2 hatványkitevő helyett kicsit kisebbre, kb. 1,98-ra voksoltak.

 Ebben az időben Einstein frissen diplomázott fizikatanár volt, ámbár e vonatkozásban munkanélküli. Szerencsére kapott állást, ügyintézőként dolgozott egy szabadalmi hivatalban. Mindeközben dicséretes módon aktívan követte a fizika aktuális problémáit, többek között az anyagban rejtőző energia kiszámítására irányuló erőfeszítéseket is. Alig néhány hónap alatt készítette el korszakos dolgozatát, melyben eljut az E=mc² képlethez. Ez telitalálatnak bizonyult. Ámde látni fogjuk, hogy a levezetés logikája problémás, mélysége pedig elégtelen. 

A következőkben megpróbáljuk megkeresni a nagyon fontos, azonban gyanúsan egyszerű képlet mélyebb alapjait.  Ezt egymás után kétszer is megtesszük.  Először egy elvontnak tartott, sok ellentmondást felmutató területen, a fény kategóriájában. Másodiknak az un. kézzel fogható anyagok világában. Érdekes módon az elvontabb terület az egyszerűbb, ezért ezzel fogjuk elkezdeni az analízist. 

            

 A fény egy nehezen kezelhető valami. A fénysugár nem térül el a legerősebb elektromos vagy mágneses térben sem, továbbá nincs hatással rá sem egy keresztbe haladó, sem egy vele szembe haladó másik fénysugár. Anyagban keletkezik és anyagba ütközve semmisül meg, a köztes útszakaszt pedig igen nagy sebességgel – fénysebességgel – teszi meg.  (Kivéve, amikor nem.) 

Van azonban néhány biztató jelenség, amely arra utal, hogy a fény – legalább részben – mégis csak anyagból van. Ilyen a fénysugár elgörbülése nagytömegű égitestek mellett, ami kísérletileg is kimutatható.  De a gravitáció nem csak vonzza a fénysugarat, hanem lassítja is.  A sebességcsökkenés akár 30% is lehet, például egy pulzár közvetlen közelében.  Ismert, hogy jelentős sebességcsökkenés szokott bekövetkezni akkor is, ha a fénysugár átlátszó anyagi test belsejében halad. 

 Mindezek után nem csoda, ha a tudomány bizonytalan a fény lényegének körülírásakor. Az újkori fizika először részecskének mondta, azután hullámnak, majd megint részecskének.  Volt olyan elmélet, melyben a mágneses és az elektromos hullámok egymásra merőleges síkban fáziseltolásban haladnak. No de miképpen tartják a kapcsolatot a semmin (a 20. századi fizika üres vákuumán) keresztül?

   

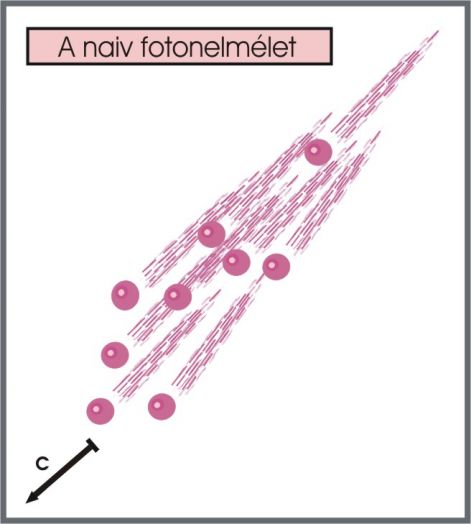
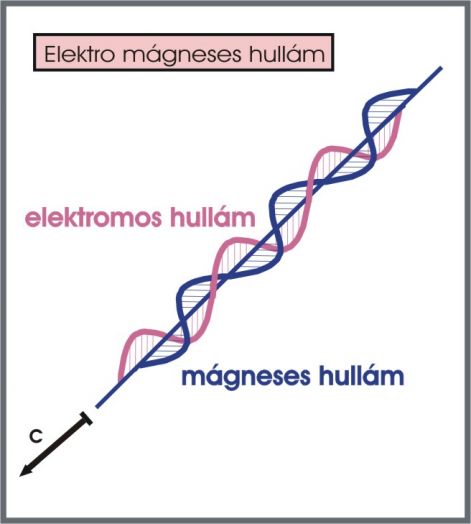
Sajnos ez az elmélet sem életképes. Hivatalosan is elvetették. Pedig kár érte, mert ez volt a szebbik azon kettő közül, amit a fizikusok ezidáig felrajzoltak. A másik a golyócska, amely valamely érthetetlen okból mindig fénysebességgel repül. 

Érdemes lenne további kísérleti eredményeket is áttekinteni, azok még több ellentmondást mutatnak. Érthető hát, hogy a tudománynak nincs konzisztens elmélete, vagy legalább részben koherens munkahipotézise. Ezért jobban járunk, ha egy általam korábban megalkotott fényelmélet mentén haladunk előre. 

Nevezzük ezt az elméletet kettős csavar fényelméletnek  (DHPT, Double Helix Photon Theory).  Két kis részecske kering egymás körül, és mindeközben előre is haladnak.  Mindkét mozgás szigorúan c sebességgel történik, így a foton-részek a vákuumban valójában 1,41c sebességgel haladnak. Ezen közben valószínűleg kondenzcsíkot is húznak maguk után, amely hullámtermészetet mutathat. Minél nagyobb energiájú fotont szül meg az atom, annál nagyobb lesz a foton tömege. Egyúttal kisebb lesz a keringés sugara, valamint a fény hullámhossza, de nagyobb lesz a kőrözés n (nű) frekvenciája.

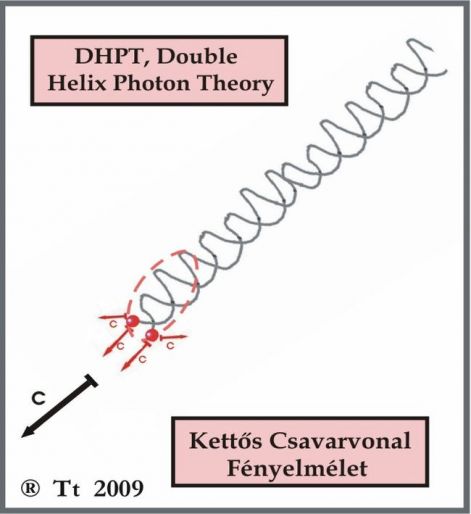
Mivel a fotonnak van impulzusa, ezért tehetetlen tömegének is kell lennie.  Sajnos, ez utóbbi becsapódáskor nullává válik és beleolvad a virtuális elektronok és pozitronok tengerébe. Így a tudósok nem találják. Ezért azután meggyőződésükké vált, hogy nincs is. 

A DHPT foton-konstrukció számos jelenségre ad kézenfekvő magyarázatot. Közöttük a legfontosabb a foton ezideig nem említett, kétszeres perdülete (szpinje). A vákuum minden egyes szubatomi részecskének biztosít egy alap-perdületet ( S₀=53*10^-36). Így a foton két részecskéjének kettőt.  E kettős részecskéből álló fotonnál tehát triviális a kétszeres szpin megjelenése. Ugyanakkor más, létező fényelméletek ab-ovo képtelenek e sarkalatos kérdést megoldani.  Így azután biztosra vehetjük, hogy a jelenleg használatban lévő fényelméletek egytől-egyig tévesek. 

Mindjárt látni fogjuk, hogy a DHPT kettős csavar fényelméletből könnyen levezethető az E=mc² energia-képlet.  A  foton fejénél lévő két kis m/2 tömeg fénysebességgel kőröz egymás körül.  Így forgási energiájuk az  mv²/2 mintájára  mc²/2.  Ezen közben előre is haladnak c sebességgel, amely további mc²/2 mozgási energiát jelent.  A kétféle energia természetesen összegződik, így a foton teljes energiája a következőképpen alakul: 

 E_foton = mc² / 2 + mc² / 2 = mc²

Tehát a fotonra – a szokásos általánosítással szólva a fényre – sikerült levezetnünk a népszerű  E=mc² képletet.  A fény azonban nem „valódi” anyag – sem köznapi, sem fizikusi értelmezésben.  Egyrészt nem „kézzelfogható”, másrészt nem fermion, hanem bozon.  Ezért tehát a fenti bizonyítás igencsak szűk hatókörű. Ugyanez vonatkozik Einstein egykori levezetésére, hiszen kizárólag a fénysugarak energiájával foglalkozott. Nagyon is eljött az ideje, hogy a képletet levezessük valódi anyagra. 

 

A hétköznapi anyagok atomokból állnak, ezen belül leginkább a protont és a neutront kell említenünk. A továbbiakban vizsgáljunk meg egy protont. Az atomfizikusok szerint ez 3 kvarkból, továbbá tömeg- és impulzusnélküli gluonokból áll.  Mivel úgy tűnik, hogy a proton külseje szilárd, ezért kell lennie valamilyen külső burkának is, bár erről mélyen hallgat a fáma.  A burok mérete 10 femto-méter, de „anyaga” még teljes homályban van.  Lehet akár anyag, akár energiamező, de tömegét 0 értékűnek veszik. 

A proton jelentős mágneses nyomatékkal rendelkezik, melynek eléréséhez a benne lévő  kvarkoknak közel fénysebességgel kell keringenie. Ez a sebesség okozza a szükséges tömegnövekedést is a kellő kvarktömeg eléréséhez. Feltesszük, hogy a 3 elektromosan töltött kvark körpályán mozog a proton belsejében. Így ezek áramgyűrűket képeznek, melyek létrehozzák a már említett erős mágneses teret. 

 Különös módon a kvarkok tömege is a fénysebességi határt idézi.  Ugyanis egy kvark tömege 300 MeV körül kell legyen, hogy a 3 kvark együttes tömege kiadja a 940 MeV értéket, a proton jól ismert tömegét. Azonban egy u kvark tömege külső térben (kvark- gluon plazmában) mérve csak 3 MeV körül van. Kézenfekvő feltételezés, hogy a hiányzó többletet a Lorentz-formula szerinti tömegnövekedés váltja ki. Egy 99,9995%-os fénysebesség éppen a szükséges 100-szoros tömegnövekedést okozza. Így 1 kvark tömege 300 MeV lesz, míg 3 kvarké cca. 900 MeV. (A további képletekben viszont elegendő pontosságot biztosít, ha egyszerűen a fénysebességgel számolunk.) 

 A kvarkok mozgási energiáját az E = mc²/2  képlet adja. Világosan látható, hogy nem jutottunk el az E = mc² képlethez. Ámbár ezt nem is remélhettük, hiszen a proton belsejében a kvarkok csak szimpla mozgást – keringést – végeznek. Van ott valami – talán a proton burka – ami megakadályozza, hogy a külső vákuum a fotonhoz hasonlóan a forgómozgást összekapcsolja a haladó mozgással.  

Joggal gondolhatunk arra, hogy a kettős mozgást (keringést és haladást) a vákuum itt is kikényszeríti valahogyan. Ha a bezárt kvarkok nem képesek haladni, akkor helyette egy mozgó vákuum-csatorna indul be az áramgyűrűkön keresztül c sebességgel, például balról jobbra. Egy ilyen mozgás a vákuum szempontjából nem probléma, hiszen szuperfolyékony. Az áramlás akár a végtelenből indul, és a másik oldalon a végtelenig tart. Közben az áramlás lágy ívekben záródik a proton körül, azaz a mágneses erővonalak képzetét idézi fel. 

 Intenzív sugárzás

 A proton belsejében keringő kvarkok elektromos töltéssel rendelkeznek – és amint láttuk – közel c sebességgel kőröznek. Ezért biztosak lehetünk benne, hogy intenzív elektromágneses sugárzást bocsátanak ki. E sugárzás energiáját az E = h * n Planck-féle képlettel jellemezhetjük. Feltételezzük, hogy csak az elektromos töltéssel bíró részecskék azaz a kvarkok sugároznak, míg az esetleges semleges részecskék nem. 

 Tegyük fel továbbá, hogy a részecskék töltés-arányosan sugároznak. Az u kvark elektromos töltése 2/3, míg a d kvarké 1/3, az egységnyi töltésre vonatkoztatva. Ezért azután az u kvarkok kisugárzott energiáját az E_u = 2/3 * h * n képlettel számoljuk, míg a d kvarkét  E_d = 1/3 * h * n képlettel. (A bizarr feltétételezések sorozatát majd a számszerű eredmények fogják igazolni.)

A kvarkok által kisugárzott elektromágneses sugarak nagyenergiájú gamma-sugarak, 10²³ Hz frekvenciával, az 1 GeV energiaszint környékén. Ezt a sugárzást ólomfal, báriumlemez avagy víztartály már nem tudja feltartóztatni. A kísérleti fizikusoknak itt esélyük sincs e sugarak energiáját kaloriméterrel detektálni. Így tehát csak az elméleti számításokra támaszkodhatunk. 

 

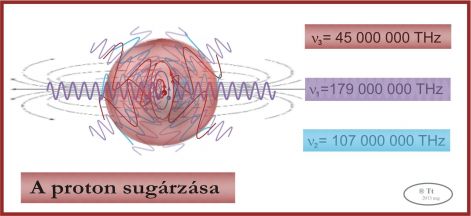
Amint fentebb láttuk, a mozgási energia a proton tömegének 50%-át adta. Ezért most azt várjuk, hogy a másik 50%-ot, azaz mc²/2 értéket a sugárzási energia teszi ki. Némi számolgatás után látni fogjuk, hogy ezt a feltételt a proton kvarkjai ki tudják elégíteni.   

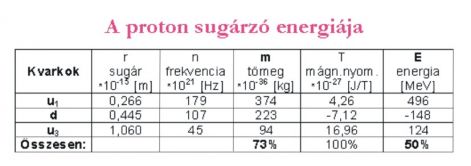
Bizonyos kísérleti eredményekhez igazodva iterációs számítással a kvarkok keringési sugarára a következő értékeket kaptam: 

 u₁:  0,267 fm,    d:  0,446 fm     u₃:  1,06 fm.

A számsorra rátekintve az lehet a benyomásunk, hogy ezek akár véletlenszerű számok is lehetnének. Azonban 3 egyenlet is behatárolja az eredményt. (Az alkalmazott iterációs számítás végén az eredmény hibája kisebb, mint 0,2%.)  Meglehet, hogy kicsivel eltérő számsor is hasonló eredményt adna, de a kvarkok sorrendjén és keringési irányán nem lehet változtatni, mert akkor a számítás elszáll.  

 A vonatkozó feltételek

1.)  Az első egyenletben a kvark szpinje (S₀) és a keringés sugara (r) szerepel.  Ezek az ismert egyenlet szerint megadják a tömeget: m = S₀ / rc 

A 3 kvark együttes tömege nem haladhatja meg a 100%-ot, és jóval 0% fölött illik lennie. A konkrét számításban ez az arány 73%-nak adódott. 

2.) A második egyenlet a keringő kvarkok által létrehozott mágneses nyomatékra vonatkozik:  T = Q*c/2r                            

Ismeretes, hogy a proton mágneses nyomatéka:                          T_p = 14,1060674333*10^-27                         Ezt a nyomatékot kell kiadnia a 3 kvarknak, bár ekkora pontosságra egyéb bizonytalanságok miatt nem szabad törekedni. Itt kell elmondani, hogy a negatív töltésű d kvark is a többiekkel azonos irányba kering,  ezért mágneses nyomatéka kivonódik. 

3.)  Feltesszük, hogy a proton energiájának hiányzó 50%-át a keringő töltések által kisugárzott energia teszi ki. Ez az energia tehát a proton energiában megadott tömegének fele, azaz 940/2=470 MeV.  A proton szempontjából elszökő gamma sugarak energiáját nem más, mint a vákuum pótolja. Ez a sugárzás adja a proton energiájának második felét, tehát egy újabb  E=mc²/2 energia-adagot. 

A fentiek alapján tehát a proton – erős általánosítással az anyag – rejtőző energiája: 

 E_anyag = mc²/2 + mc²/2 = mc²

Ez az általánosított képlet gyakorlatilag jó, bár elvileg nem igaz. Ahogyan azt a levezetésből láttuk,  a következőképpen kellene némileg korrektebb módon felírni: 

 E_proton=m_p*c²/2+E_u1(Q₁, r₁)+E_d(Q₂, r₂)+E_u3(Q₃,r₃)

Azaz a képletnek mutatnia kellene, hogy az energia több részből tevődik össze: mozgási energiából és az elektromágneses sugárzások energiájából.  

                                       Kiegészítések

  Vegyük figyelembe, hogy a nukleonok energiája csökken, amikor csoportosulnak, atommagokat alkotnak. Például amikor egy proton és egy neutron összetapad és deuteront alkot, akkor kisugároznak 2,22 MeV energiát, és össztömegük is ugyanennyivel csökken.  Amikor egy deutérium és egy trícium egyesül héliummá, akkor újra tömegcsökkenés következik be, stb.

 

 Nyilván a bevezetőben említett kődarab is csökkent energiával rendelkezik. Azonban egyenként lecsippentve szubatomi részecskéit, majd szétdobálva őket az űrbe a részecskék össztömege nagyobb, tehát az elméleti tömeg lenne. Mostanra összeállt kődarabnak, ezért tömege (belső energiája) kevesebb, mint a követ alkotó részecskéké. Mi ezt a csökkentett értéket véljük teljesnek. 

 „A p-p ütköztetések során a proton belsejében 3 gömbhéjat mértek ki. Ezek sugarai rendre 0,2; 0,44; 0,87 fm. A méréseket Islam és munkatársai végezték el a CERN-ben és a Fermi Laboratóriumban. Publikáció: 2009”

 A publikációban szerepel még egy további figyelemre méltó eredmény. Eszerint a belső gömb kemény, a középső rugalmas, a külső még inkább.  Ez jól harmonizál a kiszámított kvark tömegekkel.  Sorrendben:  375, 220 és 95 MeV.

 A hivatkozott kísérlet egy további állítása, hogy a belső  gömbben van a három vezetési kvark.  Ha ennek utánaszámolunk, akkor kiderül, hogy a kvarkok ilyetén elrendeződése nem állhat elő. A szpin-feltétel miatt 58% tömeg túllépés áll be.  Ezen közben a mágneses nyomaték még mindig 43%-al kevesebb lenne az elvárt értéknél. Tehát vagy az idézett mérés nem pontos, vagy ez az ellenőrző számítás nyugszik hiányos alapokon.

                                   Megerősítések

  Az E=mc² elméleti jóslat az 1930-as években vált realitássá. Kémikusok kimérték a radioaktív anyagok bomlástermékeit, és valóban tömeghiányt tapasztaltak. Jó magam is elvégeztem két számítást, amelyek elég nagy pontossággal megerősítik a képlet igazát. Egy un. E/E₀-arányszám előállításával két jól ismert fizikai jelenséget is leellenőrizhetünk.

Maga az E/E₀ arányszám egy olyan törtet jelent, ahol a számláló a megfigyelt energiaváltozás, míg az E₀ az anyag belső energiája. Ha ez utóbbinál helyes értékkel (E=mc²) számolunk, úgy a számítás eredménye jó egyezést fog mutatni a megfigyelt jelenségekkel. Az alábbiakban a Nap melletti fényelhajlást és a gravitációs kékeltolódást fogjuk megvizsgálni.

                           A Nap melletti fényelhajlás

  A gravitáció hatására történő fényelhajlás kísérleti mérése 1919-ben történt meg. A fizikusok a Nap melletti 1,75 szögmásodperces fényelhajlás felét tudják kiszámolni gravitációból, miközben a Nap tömegét pontosan ismerték.  A másik felét – Einsten javaslatára –  egy un. térgörbület (?) hatásának tulajdonítják. Ezzel szemben a második részt a gravitációnak a fénysugarakra ható lassító hatása adja. A Nap közelében a gravitációs térerő változó értékű, mely végtére is a fényhullámot szintén a gravitációs központ felé görbíti. A vonatkozó számítási eredmények, illetve a fénysugár görbülésének mértéke:

  Világosan látszik, hogy a fényelhajlás második összetevője igen jó pontossággal számítható az E/E arányszámból, ezen belül a képletben szereplő E=mc² összefüggésből. Mindez alátámasztja a már korábbról közismert E=mc² képletet, de egyúttal elméleti hátteret és követhető levezetést helyez mögé. Megjegyzem, hogy e jelenség bizonyító ereje nem túl magas. Ugyanis a napkorona anyaga – mint afféle optikai lencse – torzíthatja a mérést. 

                           Gravitációs kékeltolódás

  Évszázados feltevés, hogy a magasból leeső fény energiája a gravitáció hatására megnő.  Azonban a sebessége nem nőhet tovább, mivel amúgy is fénysebességgel halad, ami határsebesség. Ezért kimondták, hogy a fényhullámnak a frekvenciája nő. Ez is nagyobb belső energiát takarna. Azonban a frekvencia megváltozása logikai képtelenség, nonszensz.  Márpedig valami tényleg megváltozik. Ezt már az első, P-R (víztornyos) kísérlet is bizonyította.  Távolodó Doppler mozgatást – 750 nm/s – kellett alkalmazni ahhoz, hogy a talajszinten álló műszer érzékelőlemeze rezonáljon. 

  Valójában a kísérletet úgy kell értelmeznünk, hogy a felhasznált Fe-57 atommagok rezonancia-frekvenciája változik meg.  Fent nagyobb, talajszinten kisebb.  Az alsó atommagok számára a Doppler-sebesség kelti azt az érzetet, mintha a fény frekvenciája csökkent volna le a kívánatos értékre. 

  A csökkenés mértékét illetve a Doppler-sebességet az E/E-arányszám segítségével tudjuk meghatározni. Jelesül:

                               E_grav  / E₀ = mgh / mc²

  A fenti arányszámmal kell megszorozni a fénysebességet, és megkapjuk a Dv=750 nm/s (+/- 0,01%) kísérleti értéket. Természetesen az E₀ = mc²anyag-energia ekvivalencia képlettel számoltunk. Ha a fenti levezetésnél például E_0' = mc²/2 képlet jött volna ki, úgy annak használatával Dv' = 1500 nm/s Doppler-sebességet kaptunk volna. De a legkorábbi formula – E_0'' = mc^1,98 – használata esetén is jól látnánk az eltérést. 

 Láthatjuk tehát, hogy mind a „valódi” anyagra készített levezetésem, mind a korábbról ismert kísérleti eredmények – az általam hozzáillesztett elméleti háttérrel – megfelelően igazolják az E=mc² képlet helyességét.  Félreértés ne essék:  Einstein 1905-ös levezetése csak levezetés-imitáció volt, és a tudományos köröknek ebbe vetett erős hite adott „szilárd alapot” a világhírű E = mc² képletnek. 

 2013 aug. 20 

 

                                                                               Tassi Tamás 

         aparadox.hupont.hu

 

  

 

De addig is meg lehet nézni: 

Professzorok kritikája!

 1 Tudományos anekdota: Einstein elcsente!  Lásd itt!

 

<< Vissza                                               Tovább >>       E=mc2 1905                                                           E=mc2 1946

 

  E=mc2 röviden

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Oldal: E=mc2 2013
aPARADOXON, a természettudomány ideiglenes kudarcai - © 2008 - 2024 - aparadox.hupont.hu

Az, hogy weboldal ingyen annyit jelent, hogy minden ingyenes és korlátlan: weboldal ingyen.

ÁSZF | Adatvédelmi Nyilatkozat