aPARADOXON, a természettudomány ideiglenes kudarcai

E=mc²  1946

Aparadox 15c 

  E=mc²  1946

Albert Einstein 1905 őszén írta meg dolgozatát a tömeg és az energia egyenértékűségéről, ismertebb elnevezéssel az E=mc² egyenlet bizonyításáról. Később – 1913 és 1916 – kisebb korrekciókat végezve ismételten leközölte. Ezek közül nyilván az 1916 évi a legjobb, magam is az utóbbi változat analízisét végeztem el az előzőkben. 

     Két évtized múltával azonban Einstein úgy érezte, hogy a csillagászati aberráció jelenségén keresztül egyszerűbben bizonyíthatja a tételt. Ennek hatására született meg az 1935 és 1946 évben publikált változat. Hallgatólagosan ez utóbbit tartják a fizikusok a legjobb, tehát a végleges változatnak. Most mi is ezt a változatot fogjuk részletesen vizsgálni. 

    Tudomásom szerint az angol nyelvű dolgozatnak nincs hivatalos magyar fordítása.  Szerencsére Hraskó Péter professzor nagy alapossággal kielemezte a témát, és erről tartott értekezése a Neten is megtalálható. Ez a helyzet több szempontból is igen szerencsésnek mondható.  Prof. H.P hazánkban a relativitáselmélet doaenje, jelenleg is aktív kutatója.  Ugyanakkor Einstein összes  E=mc² levezetése – kimondva vagy kimondatlanul – a relativitáson alapul. Így tehát biztos alapokról indulunk el, míg  ezen közben a levezetés szövege nyilván célirányosan tömörített és segítő utalásokkal is ellátott. 

      Mindezen pozitívumok ellenére sem javaslom az Olvasónak, hogy egy szuszra átfussa az ominózus szöveget – abban a hitben, hogy valóban meg is fogja érteni. Olvassa inkább felszínesen, amúgy kutyafuttában – azzal a szándékkal, hogy később majd többször is vissza-vissza tér rá. Tegyen így annak ellenére, hogy a szöveg külső alakját tekintve igen színes, sőt túlzottan is színes. Föl kell áldoznunk az esztétikát az érthetőség oltárán. Sötétlila színben helyezem be Hraskó professzor ide vonatkozó előadás-részletét, világos lilával kiemelve Einstein "problémás" állításait, míg szürke színben prof. H.P  jószándékú, ámbár ugyancsak "problémás" értelmező szövegeit. 

      Íme itt következik Einstein levezetése a fentebb megbeszélt módosított formában.

A nyugalmi energia

Részlet Hraskó Péter előadás sorozatából

Mikor egy tárgyat melegítünk, az E₀ belső (vagy nyugalmi) energiáját változtatjuk. Ennek az energiának a megváltozását a csodálatosan egyszerű DE₀=Dm *c²  kapcsolja össze a tömeg megváltozásával. A DE₀=Dm*c² képletben szereplő mindhárom mennyiséget már a 19. században ismerte a fizika, de semmi jel se mutatott arra, hogy ilyen mély kapcsolat állna fenn közöttük. Alkalmas kísérletben mindhárom mennyiséget külön-külön meg lehet mérni, tehát az összefüggés helyességét tapasztalatilag lehet igazolni vagy cáfolni.

      A képlet bizonyítása a következőképpen történik. Képzeljünk el egy m tömegű testet, amely az X Y Z inerciarendszerben nyugszik. Figyeljük ugyanezt a testet egyidejűleg egy másik, X' Y' Z' vonatkoztatási rendszerből is, amelynek tengelyei párhuzamosak az X Y Z tengelyeivel és tetszőlegesen kis v sebességgel mozog a közös X-tengely mentén negatív irányba. A vesszős koordinátarendszerhez képest a test természetesen v sebességgel fog mozogni az X' tengely pozitív irányába    (5.)       ( Ld. az 5. ábrát ).

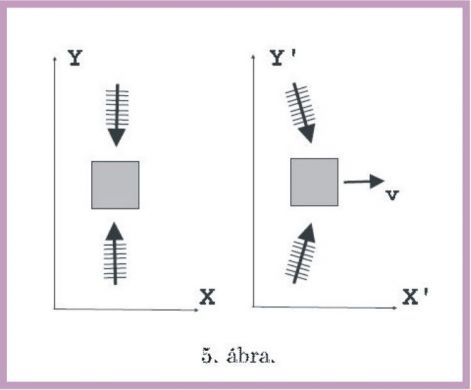
   Képzeljük most el, hogy két teljesen egyforma elektromágneses hullámcsomag esik rá a testre, amelyeket a test teljes egészében abszorbeál. (1.) Tegyük fel, hogy a két csomag a vesszőtlen rendszerben pontosan az Y tengellyel párhuzamosan érkezik egymással ellentétes irányból.

 A klasszikus elektrodinamika szerint az ilyen hullámcsomagoknak van valamekkora energiája, (e) és impulzusa (p), amelyek között fennáll az e=cp reláció.

 Az energia megmaradás tétele következtében a hullámcsomagok elnyelése után a test energiája 2e -nal megnő. Ez a növekmény azonban kizárólag a belső energiát növeli meg, hiszen a test továbbra is nyugalomban marad: Az impulzusok, amelyeket a test a két hullámcsomagtól vesz át, pontosan kompenzálják egymást.

 (2.) Az X' Y' Z' rendszerben a fénysugarak már nem ugyanazon az egyenesen mozognak, hanem elhajolnak a vesszőtlen koordinátarendszer mozgásának az irányába (4.)  (aberráció). (3.)  Az aberráció szöge az Y' iránnyal bezárt a szög. Mivel v<<c, a sebességek vektordiagramja alapján ez a szög v/c radiánnal egyenlő.

      A két csomag impulzusa most nem kompenzálja egymást, hanem 2p sin(a)= 2p sin (v/c)~2p v/c X-irányú impulzus adódik át a testnek.

A test sebessége azonban nem változik meg, hiszen a vesszőtlen rendszerben nyugalomban maradt, ezért a vesszős rendszerben továbbra is v sebességgel fog mozogni X' pozitív irányába. Hogyan változhat meg akkor az impulzusa? Csak úgy, hogy a tömege megnő valamilyen Dm értékkel.

      Mivel v-t nagyon kicsinek választottuk (elvben v →  0), ezért az impulzus még a speciális relativitáselmélet szerint is mv-vel egyenlő. A csomagok elnyelése után tehát az impulzus megmaradás tétele következtében teljesülnie kell a 2pv/c=Dm*v relációnak, amelyből a Dm=2p/c képletet kapjuk a tömegnövekedésre.

      Azonban, mint mondottuk, a hullámcsomag energiája és impulzusa között fennáll a p=e/c  reláció, így Dm=2 e/c².  De 2e a test belső energiájának DE₀ megnövekedésével egyenlő, ezért végül DE₀=Dm _* c².

      Ez a bizonyítás az energia és az impulzus megmaradásán alapul, ezért az energia és a tömeg megváltozását kapcsolja össze egymással. Azonban jó okunk van feltételezni, hogy a delták nélküli E₀ = mc² is igaz.

      A természetben pl. vannak olyan objektumok ( a p₀ mezon pl. ilyen), amelyek spontán módon elektromágneses sugárzássá tudnak átalakulni és nyugvó pionok szétsugárzásánál a létrejövő sugárzás energiája mp₀c²-tel egyenlő. Ez arra utal, hogy nemcsak a tömeg egy része kapcsolatos a test belső energiájával, hanem az egész tömeg. Az E₀ = mc² törvényt tömeg-energia relációnak nevezzük.

     A továbbiakban egy szabadon mozgó tömegpont E energiáján a mozgási és a nyugalmi energia összegét fogjuk érteni. A (18) figyelembevételével azt találjuk, hogy E = K + E₀ = mc² / gyök (1 – v² / c²)  (19) Az E₀ = mc² képlet ennek speciális esete, amely nyugvó testre vonatkozik. A gondolatkísérletben a test energiája annak következtében nőtt, hogy elektromágneses sugárzást nyelt el. A termodinamikából azonban tudjuk, hogy egy test termodinamikai állapotának a megváltozása energia felvétel során nem függ attól, milyen formában kapta az energiát. Ezért a tömeg akkor is nő, amikor a testet melegítjük. Kihatásaiban ez a relativitáselméletnek talán még nagyobb jelentőségű következtetése, mint az, hogy egyetlen test sem mozoghat fénysebességgel vagy annál gyorsabban.

      A fenti bizonyításban egyáltalán nem hivatkoztunk explicite a relativitáselméletre, ezért az ember azt gondolhatná, hogy ez a gondolatmenet a newtoni fizikán belül is érvényes. Nem így van, mert a gondolatmenetben kihasználtuk, hogy az X Y Z és az X' Y' Z' inercia rendszer még az elektromágneses impulzusok szempontjából is egyenértékű egymással. Ez a feltevés csak a relativitáselméletben jogos, mert a newtoni fizika inercia rendszerei csak a mechanikai jelenségek szempontjából ekvivalensek.

     De az igaz, hogy az eddig vizsgált problémákkal ellentétben az E₀=mc² képlet levezetésénél az idődilatációt és a rá jellemző          gyök(1- V²/c²)-t nem kellett kihasználnunk.

      A képlet bizonyítása a Lorentz-transzformáció ismeretében sem változik. Ennek az az oka, hogy a Lorentz-transzformáció (és az idődilatáció is) a kinematika körébe tartozik, míg a tömeg-energia reláció dinamikai természetű.

      Az E₀=mc² reláció egyenes következménye, hogy a tömeg nem marad meg. A belső energia ugyanis az energiának csak egy része, amelynek külön nem kell megmaradnia, és ezért a tömegnek sem kell.

     Az alfa-bomlásban pl. a bomlástermékek belső energiája kisebb, mint a bomló magé, és a különbség a bomlástermékek mozgási energiája formájában jelenik meg. De akkor a bomlástermékek össztömege is kisebb, mint a bomló mag tömege.

     A newtoni fizika alapjául szolgáló jelenségekben a belső energia változása olyan kicsi magához a belső energiához képest, hogy az ezzel együtt járó tömegváltozás is megfigyelhetetlenül kicsi (D m/m << 1).

  Ezért vált a tömegmegmaradás a newtoni fizika egyik alaptörvényévé, amely azonban pl. az alfabomlást megtiltaná. A newtoni fizika érvényességének ezért nemcsak az a feltétele, hogy a sebességek legyenek sokkal kisebbek a fénysebességnél, hiszen pl. alfa-bomlásnál ez a feltétel teljesülhet. Az is követelmény, hogy a Dm legyen elhanyagolhatóan kicsi.

   Einstein relativitáselméletről szóló nevezetes közleménye A mozgó testek elektrodinamikájához címmel 1905  júniusában jelent meg és az elmélet minden lényeges aspektusát tartalmazta egyetlen kivétellel: Csak a mozgási energiára vonatkozó (18) szerepelt benne, az E₀=mc² képlet nem. Ez utóbbi formulát Einstein még ugyanazon év szeptemberében publikálta egy rövid cikkben, amely a Függ-e a testek tehetetlensége az energiatartalmuktól címet viselte. A gondolatmenetet azonban még hosszú ideig csiszolta. Itt most az 1946-ban publikált változatot ismertettük.

 A fenti Einstein-féle levezetés alapos átolvasásának halasztását a csillagászati aberráció nevű fénytani fogalom indokolja. Ez az alig ismert, ezen belül is többnyire félreismert fénytani jelenség.  képezi az elvont levezetés alapját, ezért felelőtlen vállalkozás lenne ismeretek hiányában véleményt formálni. Szerencsére e témát egy korábbi könyvemben már feldolgoztam, melynek felhasználásával elégséges ismeretet tudok átadni.  Íme az ismertető:

A csillagászati aberráció

Fragmentumok az  EINSTEIN FELLEGVÁRA c. könyvemből

Ez a fogalom azt jelenti, hogy a csillagok valójában nem ott helyezkednek el az égbolton, ahol látjuk őket.  Eltorzult helyzetük – aberrációjuk – meglepő módon a Föld sebességének, űrbéli mozgásának  a következménye.

      A fény elhajlása, un.  aberrációja gyakran előfordul a mindennapi életben.  Átlátszó anyagokon át nézve észrevehetjük, hogy a fénysugár megtörik.  De elhajlik a fény akkor is, ha szorosan egy anyagdarab felszíne fölött halad el, vagy egy nagy tömegű égitest mellett.  A most megbeszélendő jelenség esetén azonban nincsen szó a fénysugár tényleges elhajlásáról.  A megfigyelő mozgása miatt tűnik úgy, mintha a sugár megtörne, illetve a fényforrás arrébb mozdulna. 

      Hasonló jelenséget már mindenki tapasztalt, és esetleg el is tűnődött rajta.  Ez a jelenség akkor lép fel, amikor egy mozgó autóban ülünk,   és éppen esik az eső. Hiába van szélcsendes idő, hiába tudjuk, hogy az eső ilyenkor függőlegesen esik, mégis azt észleljük, hogy bármerre nézünk ki az autó ablakain, az esőcseppek mozgását ferde irányúnak látjuk.  Ez nem érzékcsalódás.  A mozgó jármű rendszerében ez a fizikai valóság. 

     Ha kilógatunk a gépkocsi oldalsó ablakán egy  kályhacsövet függőleges helyzetben, akkor az esőcseppek nem fognak keresztüljutni rajta, a  csőfalának belső oldalát fogják verdesni.  Előre kell döntenünk a cső felső peremét, ha azt akarjuk elérni, hogy a cseppek akadálytalanul keresztül essenek rajta.  A cső megdöntésének mértéke az esőcseppek és a jármű sebességének arányától függ.

       A csillagok esetében az esőcseppeknek a csillagfény fotonjai felelnek meg, míg a mi mozgó járművünk maga a Föld.  Ha a Föld mozgásiránya éppen merőleges a megfigyelt csillag irányára, akkor pontosan az előző helyzet áll elő.  A csövet tehát előre kell dönteni a föld haladásának irányába. 

      Elsőre talán mindenki speciális optikájú csillagászati távcsőre gondol, de  lehet ez egy egyszerű irányzó eszköz is.  Egy szimpla nagyon hosszú csőre gondoljunk. 

  A cső megdöntésének mértékét a Föld és a fotonok sebességének aránya határozza meg.  A Föld keringési sebessége a Nap körül 30 km/s, míg a fotonok sebessége 300 000 km/s.  A kettő hányadosa szögérték, mégpedig radián.  E szöget (alfa) ilyen egyszerűem kapjuk meg: 

alfa=v/c  [radián] 

 Ezt a radiánban kapott szögértéket az  57,3*60*60  szorzó segítségével  számíthatjuk át szögmásodpercbe.  Esetünkben 20,4" (szögmásodpercet) kapunk.  Ez csillagászati vonatkozásban igen nagy érték, amely mellett szinte eltörpül a Merkúr nevezetes Perihélium–vándorlása (éves értéke 0,43").

      A jelenség nagysága attól is függ, hogy a megfigyelt csillag hol helyezkedik el az égbolton a Föld mozgásirányához képest.  Ha pontosan merőleges irányban van (=90 fok), úgy az aberrációs effektus teljes mértékben érvényesül, a csillag 20,4"–el előrébb látszik elhelyezkedni, mint ahol valójában van.  Ha viszont a csillag pontosan a haladás irányába esik, úgy a fényelhajlás 0, nincs aberráció.  Közbülső helyzetű csillag fényének látszólagos elhajlása e két érték között van.  Nagyságának változását a  sin(j) szorzóval vehetjük figyelembe. 

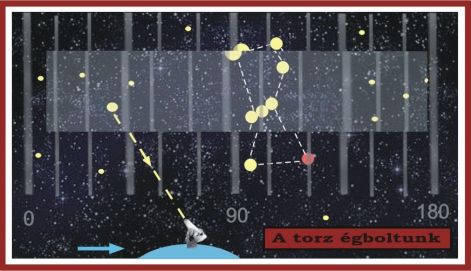
      A következő ábrán megkíséreljük síkba terítve ábrázolni az éggömb egy részletét a rajta lévő meridián–vonalak segítségével.  Az alsó és felső sáv az eredeti, azaz  a valódi helyen lévő vonalakat mutatja, a középső sáv viszont azt, amit mi emberek innen, a Föld felszínéről látunk. Kisé  Torz, vagyis hamis égboltunk van.  Maguk a csillagképek elcsúsznak helyükről, valamint el is torzulnak.

      Nos,ez a csillagászati aberráció lényege.  Azonban érdemes megismerni még néhány adalékot, mert ezek is viszonylag egyszerűek, ugyanakkor mutatják a jelenség fontosságát a csillagászatban.

     Tudjuk, hogy a Föld forog, és ebből nagyjából 0,3 – 0,4 km/s felszíni sebesség adódik, melynek nagysága és iránya folytonosan változik a megfigyelt égitesthez képest.  A Föld pályája pedig nem kör, hanem ellipszis, amely mentén Földünk változó sebességgel halad.  Ezt +/- 0,34" korrekciós tényezővel veszik figyelembe.  Ennél sokkal jelentősebb hatás, hogy a Föld folytonosan változtatja sebességének irányát, így egy csillag égi helyzete fél év alatt +20,4"–ről -20,4"–re változik. 

     Létezik még egy un. évszázados aberráció ( 13"), mert a Naprendszer sebessége eltér a közeli csillagok sebességének átlagától.  Meglepő talán, de a csillagászok mindezideig nem figyeltek fel az égbolt legnagyobb mértékű torzulására.  A Naprendszer ugyanis igen tekintélyes, 400 km/s sebességgel kering a Galaxis középpontja körül, ami 300" körüli aberrációt kell, hogy eredményezzen.  Ez azt jelenti, hogy a távoli galaxisok pozíciója jelenleg akár 300" hibával van katalogizálva.  A galaxis–aberráció nagy értéke ellenére nehezen vehető észre, mert iránya évszázadok alatt is alig változik.  Tudomásom szerint ezt az aberráció–típust eddig még senki sem mutatta ki, és nem is kereste, sőt talán nem is gondolt rá.

      Bizarr jelenség bár, de a csillagászati aberráció mértékét nem befolyásolja a megfigyelt égitest mozgási sebessége.  Ez kizárólag a megfigyelő sebességétől függ.  A relativitáselmélet nem tudja e problémát kezelni – de a kérdést most függőben hagyjuk.