aPARADOXON, a természettudomány ideiglenes kudarcai

 Ad 1. 

Két hullámcsomag

 „Tegyük fel, hogy a két csomag a vesszőtlen rendszerben pontosan az Y tengellyel párhuzamosan érkezik egymással ellentétes irányból.”

Einstein példájában egy test lebeg az űrben, és két oldalról két reflektor világítja meg. Legyen a továbbiakban a lebegő test egy autó, és ez reflektorozzon egyenlő erővel előre és hátra. Ez utóbbi esetben ugyan a test nem elnyeli, hanem kisugározza az energiát, de energia-transzfer és a sugárnyomás egyensúlya tekintetében a két eset azonos. 

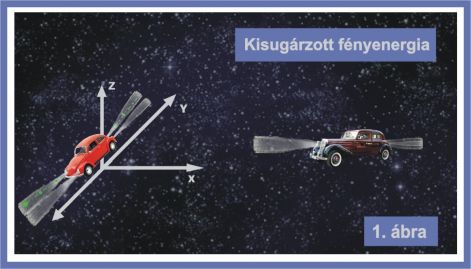
Az 1. ábrán láthatjuk a kis piros autót. Amint az x y z koordináta y tengelyén áll, és e tengely mentén reflektoroz előre és hátra. Látja ezt a másik – most még álló – autó vezetője is, ámbár nem egykönnyen látja. Ugyanis a fénysugár oldalról egyáltalán nem látható. Hacsak nem lebegnek az útjában porszemek, pollenek, spórák stb.  Ezeken minden irányban szóródik a fény, eljut a megfigyelő szemébe, és kirajzolódik a sugárkéve útja. Mi zöld szentjánosbogarakat rajzoltunk be a fénykévék tengelyvonalába, ámbár gondolhatunk lebegő zöldre festett golyócskákra is.  

 Ad 2.

 „Az X' Y' Z' rendszerben a fénysugarak már nem ugyanazon az egyenesen mozognak, hanem elhajolnak a vesszőtlen koordinátarendszer mozgásának az irányába (aberráció). „

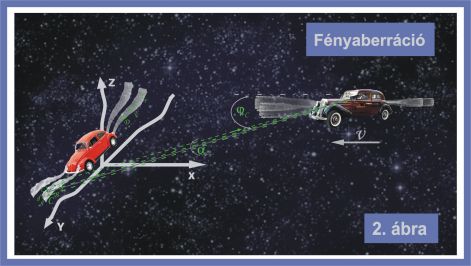
    Most vegyük tehát azt az esetet, hogy a megfigyelő autója -v sebességgel halad negatív irányban, a piros autó felé. Eközben látcsövét ráirányítja a golyókra, egyikre a másik után.  Nem a valódi helyzetükben fogja látni a golyókat, hanem kicsivel arrébb. Ez már a csillagászati aberráció jelensége, pontosan olyan, amilyet a korábbi magyarázó részben láthattunk. 

    Nem a reflektorok sugara vetődik tehát a távcső tubusába, hanem néhány szóródott zöld fénysugár, amelyek éppen a „jó” irányban haladnak. Az 2. ábrán jól látszik, hogy a C  golyót nézve a távcső nem a golyóra, hanem a mögötte megjelenő C' fantomgolyóra irányul.   

  Persze a golyócskák valójában nem mozdultak el a helyükről, mindössze a megfigyelőnek – a sofőrnek – kellett megbillentenie az irányzékot. Például a C golyó esetében az aberráció a_aC szögét így számolhatta ki: 

 a_aC = v/c * sin(j)  [radián]

      Minél közelebb néz a megfigyelő az x tengely felé, annál kisebb lesz a j_C szög, annál kisebb lesz az eltérés az a_aC aberrációs szög is. Ezért azután a golyók sora az origótól kezdődően  hátrafelé hajlik, ív alakot vesz fel. Persze minden egyéb vonal hátra hajlik, így maga az y tengely is hátra görbül. 

 Ad 3. 

 „Az aberráció szöge az Y' iránnyal bezárt a szög. Mivel v <<c, a sebességek vektordiagramja alapján ez a szög v/c radiánnal egyenlő. „

    Ritka eset, amikor a matematikusok képlet formájában hibáznak, és még ritkább, ha ez még hétköznapi emberek szemében is feltűnik. A szokásos elegáns több oldalas egyenlet-halmazokban is lehetnek hibák, főleg az input és output részeken. De ezek többnyire rejtve maradnak, hisz a látványtól leginkább menekülésre érzünk késztetést. Az Einstein által kigondolt  v/c aberrációs képlet azonban olyannyira és olyan triviálisan hibás, hogy e ponton igazság szerint véget kellene vetni minden további analízisnek.  Íme a hibás és a helyes képlet: 

  Két okunk is van arra, hogy mégis csak tovább nézegessük Einstein elhibázott levezetését.  Egyrészt érdekes lehet végignézni, hogy milyen féligazságok és vargabetűk mentén sikerül neki eljutni a helyes végeredményre. Másrészt magam is levezettem a képletet, és bár a fotonoknál egyező eredményre jutottam, de a fermionokra vonatkozó levezetésnél kétségeim támadtak. A téma kiemelkedő jelentősége miatt igenis érdemes minél többször végig gondolni és elemezni ezt a nagyon fontos képletet. 

Ad 4.

 „(aberráció)”

Megfigyelhetjük, hogy a virtuális golyósort összekötő g' görbe az autónál belesimul az y tengelybe. Így azután a reflektorokból kilépő fénysugarak impulzusának nincs x irányú összetevője. Ráadásul ezek csak látszólagos, azaz fantom sugarak. Ezen közben a valódi reflektor-sugaraknál semmi változás sem történt, folyamatosan a g egyenes mentén, az y tengellyel párhuzamosan haladtak.  Ezekből a fénysugarakból pláne, hogy nem származhat x irányú impulzus, hiszen nincs x irányú összetevőjük. 

 Ad 5.

Ld. a Hraskó-féle 5.ábrát.

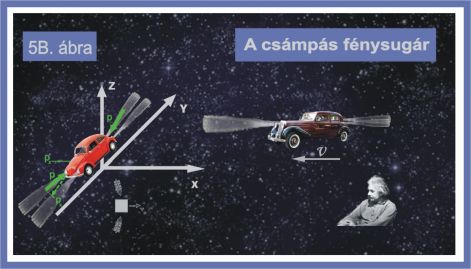
Einsten szövegét feltehetőleg Hraskó Professzor egészítette ki az 5. ábrával. Annak jobb oldali részén látjuk a testet „mozgó” állapotban. Mármint a megfigyelő szemszögéből, aki éppen azt képzeli, hogy ő maga áll, és az álló test mozog. Az ábrán egyenes vonalban haladó fénysugarakat látunk, melyek ferdén érkeznek a test tetejére és aljára. Nézzük meg eme fantázia által teremtett elképzelést a jobb minőségű 5B ábrán is. 

     Így már jobban látszik, hogy ez az optikai sugallat egy minden alapot nélkülöző téveszme.  Ilyen éles szögben megtört sugárkéve sosem hagyhatja el az autó reflektorát. Mint fentebb láttuk, a csillagászati aberráció nem ilyen. Einsten bizonyára hallott eme ominózus fogalomról, és egyből érteni is vélte. Ábrát – nyilván, és szokása szerint – nem készített.  Szerencsénkre Hraskó professzor segítségünkre sietett, pótolta a hiányt, ezzel is oszlatva a ködöt. Viszont Ő sem vette észre, hogy az egész úgy téves, ahogy van. Mindazonáltal bizton sokan irigylik H.P professzort, mert Ő itt egy szintre került a világhíres tudóssal.     

 Az aberráció latin szó, elhajlást elgörbülést jelent.  Önmagában állva túlzottan általános jelentésű szó, sokféle szakterület használja fel más-más értelemben. Még a fizikán belül is többféle hatásra vezethető vissza, melyeket  mind fényelhajlásnak illetve aberrációnak nevezhetünk.   E kifejezést könnyedén odavetve egy nehéz levezetésben a triviális magyarázat és a korrekt lezárás illúzióját kelthetjük vele. 

      Nagy a baj azonban – mint esetünkben – ha maga a fogalom használója sem érti, sőt félreérti.  De még nagyobb baj az, ha eltelik 7 évtized a tudományos életben, és senki nem jön rá, hogy egy magasan jegyzett tudományos dolgozat kiinduló pontja alapvetően téves. A korrektség is azt diktálná, hogy az elkövetett hibát a tudományos közösség mihamarabb korrigálja.  Miért is nem tette eddig?  A számos ok közül az egyik az alapvető ismeretek hiánya néhány szűk, de mégis nélkülözhetetlen szakterületen. Sajnos ilyen látens hiány gyakorta előfordul.