Tassi Tamás

         A "modern" fizikáról klasszikusan és közérthetően.      

 

 

A fiatal angol csillagász, Arthur Eddington igen szorult helyzetbe került, mert ő is megkapta a harctéri behívót. Börtön várt rá, lévén kvéker, így vallásilag pacifista. Megmentése érdekében napfogyatkozás expedíciót szerveztek Principe szigetére, persze Eddington vezetésével. Tették ezt annak ellenére, hogy mindez egy ellenséges ország tudósának (bizonyos Einstein úrnak) a javát szolgálta.

 

Eddington feladata lett lefotózni az 1919 május 29.-i napfogyatkozást, bizonyítandó, hogy a Nap elgörbíti a fénysugarakat. Tényleg elgörbítette. A világ népei tapsoltak, lelkesedtek. Elsősorban is a megkönnyebbülés miatt, hogy végre vége a szenvedéseknek, a véres háborúnak. Továbbá mert jó volt hallani, hogy a korábbi ádáz ellenségek összefogva valami békés és talán értelmes tevékenységbe kezdtek. Ezt a pillanatot elmulasztva egy későbbi alkalom már nem kapott volna kiemelt figyelmet, nem hozta volna meg a relativitás-elmélet mindent elsöprő sikerét.

Newton bő három évszázaddal ezelőtt munkálkodott. Már Ő is gondolt arra, hogy a fény pályája nem mindig egyenes. A fényt apró golyócskáknak gondolta, amelyre hat a Nap gravitációs ereje. A repülő golyócskák elhajlása annál nagyobb, minél közelebb halad el a Naphoz, elvileg érinti a felszínét.  Ez a távolság a geometriai központtól  R=700 000 km. 

A Nap tömegének (M=2*1030kg) és a gravitációs állandó (G=66,7*10-12) ismeretében kiszámították a fénypálya szögelhajlását. Ez 0,85 szögmásodperc körüli értéknek adódott. Ennél a számításnál már figyelembe vették a fény különleges tulajdonságát, mely szerint a Nap vonzóerejének hatására nem gyorsul fel, hanem útja során végig megtartja állandó c sebességét.  Eközben a Nap folytonosan maga felé húzza a fotonokat, azaz görbíti a fénysugár pályáját. Láthatjuk, hogy itt a fotonok szolid apró kavicskáknak tűnnek, melyek anyagszerűek, van gravitáló hajlamuk, és akkor bizonyára van tehetetlen tömegük is. Csakhogy van valami rejtélyes dolog az űrben, ami lekorlátozza sebességüket. A gravitációs hatás változó intenzitású, a távolban gyenge, a Nap közelében a legerősebb. Az eltérítő hatások összege pontosan annyi, mintha a fotonokat 2R szakaszon vonzaná a Nap, de ekkor folytonosan maximális intenzitással. 

Nem csak a Newton féle fényelmélet hívei kapták eredményül a 0,85 szögmásodpercet, hanem később Einstein is. Ezt 1911-ben számolta ki alakulófélben lévő általános relativitáselmélete segítségével. 1915-ben újraszámolta, és a kétszeres érték mellett döntött. Ez utóbbi jóslat birtokában indult el az angol csillagászati expedíció az 1919-es napfogyatkozás megfigyelésére Eddington vezetésével. A kiértékelő bizottság - a zavarok leküzdése után - az 1,7" értéket fogadta el. A fotók ugyanis nagyon rossz minőségűek voltak. A  napfelszín közelében sokminden akadályozta a csillagfény zavartalan haladását. Említendő a napkorona anyaga, a flerek, a dzsettek stb. A zavaró tényezők másik csoportja a forró trópusi légkör, a láthatatlan légörvények, légbuborékok, remegések. Így a Nap közeli csillagok fénypontok helyett elmosódott pacáknak tűntek.

Amennyire sikeres volt Einstein jóslata, annyira problematikus a jelenséget magyarázó elméleti indoklása. Hibrid megoldást alkalmazott. A fénypálya elhajlásának felét Ő is a Nap vonzó hatásának tekintette. Az elhajlás másik felét viszont egy speciális, általa megalkotott geometria hatásának tulajdonította. Feltételezése szerint a nagy tömegű gravitáló testek meggörbítik a környező teret, és a kisebb testek valamint a fény mozgásuk közben ezt a görbületet követik.

„Az elmélet szerint az elhajlást felerészben a Napnak (newtoni) - vonzótere, felerészben pedig a térnek a Naptól eredő geometriai módosulása („görbültsége") okozza.. "

 A. Einstein 

Az 1,7" eltérülés másik felét sokkal egyszerűbben, ráadásul a görbült tér absztrakcióját elkerülve, a  hagyományos fizika talaján állva is meg lehet magyarázni. Ennek érdekében egyetlen feltételezést kell tennünk. Jelesül azt, hogy a gravitációs energia csökkenésével a fény sebessége is csökken. Mint tudjuk, a gravitációs energia a végtelenben a legnagyobb. A fizika jelölése szerint ott 0 (nulla), míg egy égitest felé közeledve értéke a 0 alá csökken, azaz a negatív tartományba kerül. 

Ikerparadoxon, Lánczos Kornél, űrrakéta,

Vegyünk gondolatban egy m=1 kilogramm tömegű testet. Vegyük hozzá, hogy a gravitációs gyorsulás a Nap felszínén 272 m/s2.  Ennek helyzeti energiája h = 1 méter magasságban E = mgh = 1*272*1 = 272 J.  Ezt az energiát át tudjuk számítani tömegre, ha osztjuk c2-el. Ha még elosztjuk a kiinduló m=1 tömeggel is, akkor egy fajlagos arányossági számot, a Dm/m -t kapjuk.

Ez egy mértékegység nélküli arányszám. Nevezzük ezt degressziós képletnek vagy csökkenési képletnek:

A képlet számított értéke 3,02*10-15 a nap felszínére vonatkoztatva. Ennek segítségével meghatározhatjuk az 1 méter magasság-különbségen jelentkező Dv sebesség-különbséget. Ez 907*10-9 m/s -nek adódik.

   Ez a sebesség-különbség csak szorosan a Nap mellett maximális értékű, távolabb egyre kisebb. A változó Dv értékeket illetve az ebből származó kis útkülönbség szakaszokat akár összegezhetnénk is egy bizonyos matematikai módszerrel. Ehelyett könnyítésként ismét úgy számolhatunk, mintha állandó Dv sebesség-különbség jelentkezne 2R útszakaszon. A sebesség-különbség és a futási idő szorzata megadja az útkülönbséget: Ds=Dv*2R/c=4,235 mikrométer. Ez az útkülönbség ugyan rendkívül kicsiny értéknek tűnik, de mindjárt látni fogjuk, hogy szépen kiadja a fénysugár várt szögelhajlását. Ezt a bizonyos szögelhajlást pedig úgy kapjuk meg, ha a Ds útkülönbséget elosztjuk a h=1 magasság-különbséggel: Ds/h=4,235*10-6 radián.

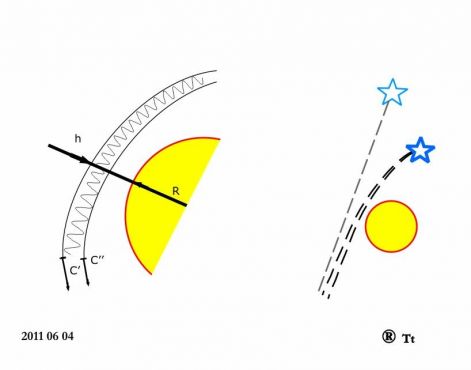
   A fenti radián-értéket át tudjuk számítani szögmásodpercre, és ekkor 0,8735" értéket kapunk. Véletlenül(?)   éppen annyit, amennyit a hagyományos gravitációs vonzás esetében is kaptunk. A Nap melletti tényleges fényelhajlás számított értéke a kétféle érték összege lesz.  (Ennek a számnak a pontossága kizárólag az adatok pontosságától függ.):              

1,7470"

Az Olvasó jogosan kifogásolhatja, hogy a számításokban szereplő h magasság ötletszerűen kapott értéket. Ez azért nem probléma, mert a szögelhajlás képletéből a h végül is kiesik. (Egyszer szorzóként, egyszer osztóként szerepel.) Mindez azt mutatja, hogy a sebesség-különbségből adódó fényelhajlás nem függ a fény amplitudójától illetve hullámhosszától. A képlet levezetéséből levonható következtetés egyezik a csillagászati megfigyelésekkel, melyek szintén azt mutatják, hogy a gravitációs fényelhajlás során nem lép fel a fehér fény színekre történő bomlása. Márpedig ilyen megfigyelések egyre nagyobb számban fordulnak elő. A csillagászok nem csak a Nap mellett, hanem láthatatlan objektumok mögötti kvazárok esetén, sőt sötét anyag felhők környékén is jeleznek markáns fényelhajlást, többnyire csillagászati objektumok kettős megjelenése formájában.

Az itt ismertetett elmélet egyszerűsége, érthetősége valamint a klasszikus fizika használata miatt mindenképpen minőségi előrelépést jelent a Nap melletti fényelhajlás problémakörében. Vessük össze ezt az egyszerűséget az einsteini egyenletek bonyolultságával, melyek talán csak szakmai körökben ismertek, és semmiképpen sem publikusak. A fentiekben sikerült a fényelhajlás jelenségét kizárólagosan, 100%-os mértékben klasszikus fizikai elvek segítségével magyaráznunk. Jelesül a Nap melletti kettős fényelhajlást a gravitációnak és a változó gravitációs energia által okozott változó fénysebességnek tulajdoníthatjuk. Ily módon nem marad hely az elméletek síkján a nagy tömegű testek által okozott un. térgörbület teória számára.

A jelenség mélyebb magyarázatát a szuperhúr elmélet adhatja meg.  Eszerint a világűrt kitöltő rezgő húrok igen nagy belső mozgási energiával és egyben igen magas hőmérséklettel rendelkeznek. A húrok átlagos mozgási sebessége határozza meg a foton haladási sebességét. Az anyagi testek valószínűleg energiát nyelnek el, a közelükben a húrok kisé lehűlnek. Ott tehát kisebb a belső mozgásuk, ezért kisebb sebességgel hajtják előre a fotonokat. Másképp fogalmazva a fény sebessége lecsökken, ha gravitációs mezőbe kerül.

Ne felejtsük el megemlíteni, hogy a valóban sikeres és nemzetközi hírnévnek örvendő expedíció, valamint az ebből főnix madárként életre kelő merész tudományos elmélet (relativitás), no meg az angol királynő kegyelméből Eddington neve és rangja fölfelé ívelt. Manapság már Sir Arthur néven tisztelhetjük.

 

Tassi Tamás

www.aparadox.hupont.hu

óra, paradoxon, Einstein, idődilatáció, relativitás, sebesség, cézium, atomóra, Hafele, Keating, kísé

E cikk eredetijének nyomtatható változata A4-es jpg formában elérhető a   következő helyen:

 

                      

    1. oldal                                      2. oldal

c

óra, paradoxon, Einstein, idődilatáció, relatív, sebesség, cézium, atomóra, Hafele, Keating, kísérlet, Kelly

Kiderült, hogy a Roswelli ufo katasztrófa valóban megtörtént:

 02 <<  Vissza  03  Tovább  >>  04 

Uri Geller James Randi parafenomén kanálgörbítés 

 

óra, pa

 

* * *

Müködik egy vitafórumom is egy másik honlapomon. Ennek neve:Gravitációs kékeltolódás, ami lényegében a gravitáció mibenlétével foglalkozik. Ha van kérdésed vagy véleményed, akkorkattints ide!

* * *

 

 

 

radoxon, Einstein, idődilatáció, relativitás, sebesség, cézium, atomóra, Hafele, Keating, kísérlet, Kelly

 

két üres sor

két üres sor

 

 

 

A fiatal angol csillagász, Arthur Eddington igen szorult helyzetbe került, mert ő is megkapta a harctéri behívót. Börtön várt rá, lévén kvéker, így vallásilag pacifista. Megmentése érdekében napfogyatkozás expedíciót szerveztek Principe szigetére, persze Eddington vezetésével. Tették ezt annak ellenére, hogy mindez egy ellenséges ország tudósának (bizonyos Einstein úrnak) a javát szolgálta.

Oldal: Kettős fényelhajlás
aPARADOXON, a természettudomány ideiglenes kudarcai - © 2008 - 2024 - aparadox.hupont.hu

Az, hogy weboldal ingyen annyit jelent, hogy minden ingyenes és korlátlan: weboldal ingyen.

ÁSZF | Adatvédelmi Nyilatkozat