aPARADOXON, a természettudomány ideiglenes kudarcai

Repülő órák

 - Aparadox  7C -

H. Lorentz holland fizikus az 1890-es években jutott el arra a következtetésre, hogy az anyagi részecskék tehetetlen tömege a sebesség hatására növekszik.  Sőt, a fény sebességéhez közelítve minden határon túl növekszik.  Egykoron levezetett képlete, az un. Lorentz-faktor ezt egzaktul követi és világosan mutatja.    Ez a tömegnövekedés a köznapi ember számára is evidencia,  hiszen a scifi könyvekből tudja, hogy az űrrakéta tömege végtelenre nő, ha át akarja lépni a fénysebességi határt.  Sokan hallottak már a részecskegyorsítók problémájáról is, hogy növekvő sebességek mellett egyre nagyobb mágneses térerő kell a körpálya megtartáshoz. 

   Mindezek fényében nem meglepő,  hogy az atomórák  járása lelassul.  Még is meglepődünk, sőt igencsak hitetlenkedünk, amikor először halljuk hogy  pusztán a sebesség hatására  egy óra képes lassabban  járni.  Netán – tán  homokszem került a tudományos ismeretterjesztés, valamint az iskolai oktatás gépezetébe, hogy ezt a színes jelenséget nem lobogtatják és nem tanítják?  Később látni fogjuk, hogy a tudomány szemszögéből ez esetben hallgatni arany.

   Az az igazság, hogy az óralassulás kapcsán egyszerre két súlyos probléma merül fel a tudomány számára. Az első a tömegnövekedés, és már ez is tökéletesen érthetetlen a ma tudósai számára.  A megszokás miatt azonban ezen az akadályon egy vállrándítással mindenki keresztüllép. 

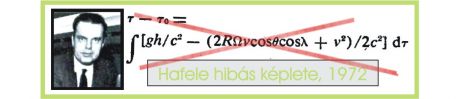
Súlyosabb gond az, hogy az eredeti kísérletben az eredmény zavaróan aszimmetrikus volt. Az 1971-eskísérletben  két ifjú tudós – Hafele és Keating – repítette az órákat Földkerülő pályán.  Menetrendszerű utasszállító gépeken repültek, cikk-cakk vonalban,  átszállásokkal megszakítva a folyamatot.  Az Egyenlítő egy végtében való megkerülése nyilván elérhetetlen célkitűzés lett volna számukra.

   A kísérleti repülés a Föld körül, először keletnek, azután nyugatnak történt.  A Hafele által várt eredmény -198 ns késés, illetve +96 ns sietés volt.

   Hafele egy újabb évre beleásta magát a relativitás, azaz  az SR és GR rejtelmeibe.  Egy általános képlettel és 6 szám-eredménnyel tért vissza a tudományos életbe.  Ebből 2 szám a magasságból adódó órasietés volt, 2 a már említett sebességből számított órakésés, 2 pedig az összegük.   Ez utóbbiak jól, (gyanúsan jól) egyeztek a visszatérő gépek órái által mutatott értékekkel.   ( A kísérlet messze nem ütötte meg az elvárható tudományos nívót.

  Mégis nyugodtan eltekinthetünk a manipulált óráktól és egyéb ügyeskedésektől.  Azóta további  megbízható kísérleteket is végeztek, melyek meg erősítették az elsőt.)

  Nem csak a H-K kísérlet számeredményei állnak ingoványos talajon. A Hafele által készített képlet elvileg hibás és pontatlan.  Álljon azért e helyen, hátha valakinek mégis ebben van bizodalma, és az elkövetkező példaszámításokat ezzel kívánja le ellenőrizni.

  A továbbiakban 6 egyszerűsített példát tekintünk át, melyek remélhetőleg jól rá világítanak a Hafele – kísérlet mögött meghúzódó fizikai problémákra, azok értelmezési és alkalmazási nehézségeire.

1/6 kísérlet

 3 atomóra a Póluson

Óra reset álló helyzetben

Tegyünk 3 atomórát egymás mellé, pontosan az Északi Pólusra. Hangoljuk a járásukat egyformára. Az 1 napi időtartam pontos hosszát a csillagászok adják meg.

    A Föld sziderikus forgási ideje 23h 56m 4,1s. Ezt a csillagászok úgy mérik, hogy a szálkeresztben megnéznek egy csillagot, majd másnap éjjel újra leolvassák az átvonulás idejét. Ez az időtartam a fentebb említett 23h 56m 4,1s. Ezt extrapolálják a csillagászok a szinodikus napra, 24 órára, azaz 86400 másodpercre.

   Az Északi Póluson a föld felszínének nincs sebessége, tehát az órák sebessége és mozgási energiája 0.

  Most helyezzük el az 1 jelű (kék) órát egy szuperszonikus vadászgép fedélzetére, míg a 2 jelű (lila) szubminiatűr órát egy lövedékbe.  Ezt a vadászgép fogja kilőni.

    Tegyük föl, hogy a gép v₁ = 500 m/s sebességgel repül, és kilövi a lövedéket 1000 m/s sebességgel. Így a lövedék teljes sebessége  v₂ = 1500 m/s lesz. Az atomórák stopper-üzemmódban egyszerre indulnak egy rádióimpulzus vagy egy GPS műholdjel hatására, majd egyszerre állnak le T=10 másodperc múlva a második impulzus után. A H-K kísérlet fényében arra számítunk, hogy a sebesség hatására az 1 és 2 óra néhány pikó-szekundummal  (10^-12 s) kevesebbet fog mutatni.

   A számítás alapja az E = mv²/2 mozgási energia  és az E = mc² anyagi energia aránya.        

   A D_E/E energiaváltozási arányszám. (A képletek végén szereplő 10^-12 szorzó végzi az átszámítást szekudomról pikoszekundum mértékegységre.)                             

DT₀ = 0[ps], Póluson hagyott fehér óra.

DT₁=D₁*T=-(500²/2/9e16*10*10¹²)=-14[ps],kék óra.

DT₂=D₂*T=-(1500²/2/9e16*10*10¹²)=-125[ps],a lila óra

A képletek ellőtt lévő mínusz előjelek azt jelzik, hogy az órák a sebesség hatására késnek.

   Mindez azt jelenti, hogy egzaktul ki tudtuk számolni a két mozgó óra késését: 0, -14, -125 ps. Ez a számítás annyiban haladja meg Hafele egyenleteit, hogy itt nem közelítő, hanem egzakt számértékeket kaptunk. De aki Hafelében hisz az számoljon utána!

 2/6 kísérlet  

3 atomóra a Póluson

Óra reset a repülőn

 Számítási bázis a relatív 0 sebesség

Vannak olyan elméletek – ilyen a rel is – melyben szabadon kijelölhetjük, hogy melyik test van nyugalomban és melyik az amelyik mozog. Tekintsük most  a repülőgépet nyugalmi állapotban lévőnek! Helyezzünk mellé egy kék színű „álló” koordináta-rendszert, amelyben tehát a gép nyugalomban van. Ebben a sebessége v₁ = 0. Persze ekkor a pólus v₀ = -500 m/s -el hátrál. A lövedék sebessége pedig v₂=1000 lesz. 

    Tegyük az órákat a repülésben lévő gép fedélzetére, és szabályozzuk be újra. Még emlékszünk rá (1/6 kísérlet), hogy ide kerülvén az óra minden 10 másodpercben 14 pikó-szekundumot késik, ezért nyilván gyorsítani kell őket. A pontos járás beállítását bízzuk ismét a csillagászokra. A pontos idő továbbítása akár GPS műholdak segítségével is történhet. 

    Most helyezzük a fehér órát a pólushoz, a lilát pedig a lövedékbe, és ismételjük meg a T = 10 másodperces kísérletet. 

 A korábban levezetett D_E/E=v²/2c² alapképlet segítségével végezzük el ismételten az elméleti számításokat. 

DT₀=D₁*T=-(-500)²/2/9e16*10*10¹²=-14[ps], fehér óra

DT₁ = 0[ps], kék óra a repülőn

DT₂=D₂*T=-(1000²/2/9e16*10*10¹²)=-56[ps], lila óra

A kísérlet végeztével most azt látjuk, hogy a póluson álló fehér, 0 jelű óra késik -14 ps-t, a repülőgép 1 jelű kék órája természetesen 0 késést mutat, míg a lövedék 2 jelű órája -56 ps-t késik. 

   Az előző kísérletben ezek egészen más számértékek voltak: 0, -14, -125

    Félre értés ne essék, ezek valódi, maradandó óra-elállítódások. Továbbá ezek megvalósítható kísérletek ha szükséges, akkor minden technikai nehézség elhárítható. Természetesen itt csak elméleti alapon tárgyaljuk a problémát.

   Már e példából is jól látszik, hogy nem lehetséges az "álló" koordináta-rendszert megválasztani. Akinek ez még nem világos, azt meg fogják győzni a következő példák.

  Érdemes talán egy pillanatra visszautalni az eredeti 1971-es H-K kísérletre. Abban a kísérletben a keleti irányba tartó repülőgép órája leszállás után valódi, -59 ns késést mutatott. A nyugatra tartó repülés befejezése után a leszálló gép atomórái átlagosan +275 ns sietést mutattak. Hafele ezt a számértéket úgy osztotta meg, hogy a magasság hatásának +179 ns sietést tudott be, míg a   sebesség hatásának +96 –ot.

    Akinek a H-K kísérlet nem tűnik  elég megbízhatónak, az tudjon róla, hogy azóta további négy kifogástalan kísérlet történt. Ezek közül a leg kevésbé autentikus a London- Sydney -London jubileumi kísérlet. Ezzel kívánták megünnepelni a H-K kísérlet 25. évfordulóját. Ez azt jelenti, hogy a tudományos világ mélyen elkötelezte magát Hafele és a H-K kísérlet „igazsága” mellett.

3/6 kísérlet 

3 atomóra a Póluson

Óra reset a repülőn

Számítási bázis az abszolút 0 sebesség

A 1/6 példában adva volt 3 sebesség; 0; 500; 1500 ms. Továbbá kiszámoltunk 3 órakésést; 0; -14; -125 ps. Ez a számsor azt a feltételezést takarja, hogy a Pólus nyugvó helyzetben volt egy láthatatlan mezőhöz képest. A repülőnek és a lövedéknek is ehhez képest volt sebessége. 

    Most végezzük el a számítást annak tudatában, hogy az órákat a mozgó repülőgép fedélzetén szinkronizáltuk. E folyamat kezdetén mindhárom órának v₁=500 m/s sebessége volt, ennek megfelelő mozgási energiatöbblettel és  -14 ps késéssel 10 másodpercenként. Történt meg a reset, az órák beszabályozása a csillagászati időre, majd a fehér és lila óra kihelyezése. 

   Számítás a Pólusra kihelyezett fehér órára: 

DT₀=–(v₀²–v₁²)/2c²=

–(0²–500²)/2/9e16*10*10¹² =+14 [ps] 

 Azaz a Pólusra kihelyezet 0 jelű fehér óra sietni fog, hiszen mozgási energiája lecsökkent a gépből való kihelyezése után. Ha véletlen szerűen bár de óra-sietéssel találkozunk, abból biztosan következik, hogy az óra beszabályozásának helyén többlet-energia volt jelen.

   Az 1 jelű kék óra 0 változást mutat, hiszen ez a gép fedélzetén maradt változatlan viszonyok között:

 DT₁ = 0 [ps]

 A lövedékbe helyezett 2 jelű lila óra sebessége: v₁+v₂=500+1000=1500 m/s. 

 A DT₂ képlete tehát így alakul:  

DT₂ =–((v₁+v₂)²–v₁²)/2c²*T*10¹²=

=-((v₁²+2v₁v₂+v₂²)– v₁²)/2c² *T *10¹²= 

= -(2v₁v₂+v₂²)/2c²*T*10¹² = 

=–(2*500*1000+1000²)/2/9e16*10*10¹²=

=-111 [ps]

A (v₁+v₂)² a lila óra össz-energiájára jellemző mennyiség, de ebből le kellett vonni az óra  v₁² kezdő energiát. A v₁² -el történő egyszerűsítés lehetőségéhez a véletlenek szerencsés találkozása kellett, lévén a kísérlet helye éppen a Föld forgástengelyén. 

   Ha összevetjük az 1/6 és a mostani 3/6 kísérlet számsorát, akkor felismerhető, hogy egy tőről fakadnak: 

                     0;    -14;     -125     [ps]

 Látszik, hogy  14 ps  lineáris eltolás van a két számsor között. Csakhogy ezen beszédes eredmény kiszámításához szükség volt a valódi sebességek ismeretére azokon a helyeken, ahol az órákat lenulláztuk. Ez a sebesség az 1/6 esetben, a Póluson 0 volt, itt, a 3/6 esetben, a repülőgépen 500. A számítások pedig csak abban az esetben harmonizálnak a fizikai valósággal, ha eltaláltuk az órák beszabályozására szolgáló mozgó test valódi sebességét. A találomra felvett sebességekről sorra be fog bizonyosodni, hogy alaptalanok és tévesek. A helyes számítás igényli az abszolút 0 sebesség ismeretét.

4/6 kísérlet 

3 atomóra Washingtonban, irány Kelet

Óra reset a földön

Számítási bázis az abszolút 0 sebesség

Erősen közelítünk az eredeti   H-K kísérlethez, ha az órákat Washingtonban (39,5  szélességi fok) szinkronizáljuk. Azaz járásukat itt szabályozzuk be a csillagászati idő ritmusához. Ebben az esetben az óráknak folyamatosan 370 m/s rejtőző sebessége van, mert Washington ezzel a sebességgel rohan kelet felé. 

   Az amerikai repülőgép (Tomcat, azaz kandúr) sebességét  370 m/s-nek vesszük, az 5/6 kísérlet érdekében is. Ha az órák kezdetben sebesség-mentes területen, ­­– például a Póluson – lettek volna beállítva, akkor a Washingtoni Időközpont technikusai ösztönösen  10 másodpercenkénti +8 piko-szekundum ritmussal gyorsabbra állították volna őket.

    A beszabályozott órák közül az 1 jelűt a repülőgép fedélzetére, a 2 jelűt a lövedékbe helyezzük. A megfigyelő számára a repülőgép sebessége  v₁' = 370, míg a lövedék sebessége  v₂' = 1370 m/s lesz. A rejtőző sebességet is figyelembe véve azonban a repülőgép sebessége valójában v₁ = 740, míg a lövedék sebessége v₂ = 1740 m/s lesz. A fizikai valóságot ez utóbbi sebességek képviselik. 

    A további számításhoz ismét a D_E/E arányossági tényezőt fogjuk használni, amely az mv²/2 mozgási energia és az mc² anyag-energia aránya:

 D_E/E = v²/2 c²

Ezen alapképlet segítségével könnyen kiszámítható a  T=10 s időtartam alatti óra Washingtoni késése: 

 DT₀ = D₀*T*10¹²= . . . = -8 [ps]

Ez a -8 ps az Időközpont óráinak elállítódása a Pólushoz képest, ami azonban nem látszik, hiszen az órákat a technikusok átállították.  Ezek az órák tehát 0 eltérést mutatnak. 

    A repülőgépbe helyezett óra késése  v1=740 m/s sebesség mellett : 

 DT1=D₁*T*10¹² – DT₀=-31 – -8 = -23 [ps] 

A lövedékbe helyezett óra késése v₂=1740 m/s mellett: 

 DT₂ = D₂*T*10¹² =-168 – -8 = -160 [ps]

A Washingtoni kísérlet nagyobb órakésései világosan mutatják, hogy a bázisnak tekintett 0 jelű fehér órának rejtőző sebessége és rejtőző energiája van.  Ennek hatása azért mutatkozik meg a relatív mozgást végző 1. és 2. óránál, mert az órakésés nem a sebességgel, hanem a sebesség négyzetével arányos:

 E_mozg =mv²/2

 Az órakésések és a sebességek a Póluson:

 0, 0ps;      500, -14ps;        1500, -125ps

A órakésések és a sebességek Washingtonban :

370, 0ps;          370, -23ps;           1370, -160ps

Az 1971-es H-K kísérlet értelmezésére ez ideig két elméleti képlet készült. Az egyik az enyém (D = v²/2c²). A másik Hafele 1972-es Science Magazine által leközölt képlete. Ez utóbbi véleményem szerint téves, sőt komolytalan.

 5/6 kísérlet 

3 atomóra Washingtonban, irány Nyugat

Óra reset a földön

Számítási bázis az abszolút 0 sebesség

Másképpen késnek az órák, ha a repülőgép nyugati irányba repül. Tudjuk, hogy  a Washingtonban hagyott fehér óra valódi – ámde rejtőző – sebessége +370 m/s keleti irányban. 

  Ugyanakkor ismerjük a repülőgép relatív sebességét, ami -370 m/s. Nagyságában tehát éppen egyezik a washingtoni óra sebességével, csakhogy ellentétes irányú. A kettő összege éppen 0, azaz kioltják egymást.  

  A lövedék relatív sebessége -1000 + -370 = -1370 lesz a talajhoz képest. A lövedék valódi sebessége tehát -1000 lesz. 

Az órák késésének számítása:

A 0 jelű fehér óra:

       DT₀ = 0 [ps]

hiszen ez az óra beszabályozás után a helyén maradt. 

Az 1. jelű kék óra:  

DT₁=-((v₀+v₁)²-v₀²)/2c²*T*10¹² =

=-(0²- 370²)/2/9e16*10*10¹²=+8 [ps] órasietés.

Valójában a nyugatnak tartó repülőgép és benne a kék óra sebessége nulla értéket vett fel, miközben a föld és a levegő 370 m/s-el elforog alatta.

Ugyanakkor a repülőgép pilótája egy igen érdekes asztrofizikai jelenséget él át. Számára megáll az égbolt, a Nap és a csillagok, és közben a Föld forog alatta. Elérte az abszolút 0 sebességet, akárcsak a Föld Pólusa. A 2. jelű lila óra relatív sebessége v_2rel = -1370 m/s. Az óra késésének számítása:

DT₂=-((v₀+v_2rel)²-v₀²)/2c²*T*10¹²=

=((-1000)²-370²)/2/9e16*10*10¹² = -48 [ps] 

Ez a lövedékbe helyezett óra nyugatnak haladva már átlépte majd meghaladta a kritikus 370 m/s határt, ezért  ritmusa újra lecsökken, újra késik. A  megmaradó sebesség ugyan negatív értékű lesz, de ettől még a sebesség négyzete, illetve a mozgási energia pozitív. Ez pedig lassítja az óra járását.

   A fenti számítás, illetve a +8 ps az eredmény jellegét tekintve harmonizál Hafele sejtésével. Őszerinte is Nyugati földkerüléskor  a sebességből óra-sietés volt várható.

   Az utasszállító gép sebessége cca. 230 m/s lehetett. Az ő kísérletében azonban a +96-os számot felülírta a magasságból eredő óra-sietés. Így a leszálló gép fedélzetén lévő órák +275 nanoszekundum sietést mutattak.

6/6 kísérlet

3 atomóra Washingtonban, irány Kelet és Nyugat

Óra reset a földön

Számítási bázis az abszolút 0 sebesség

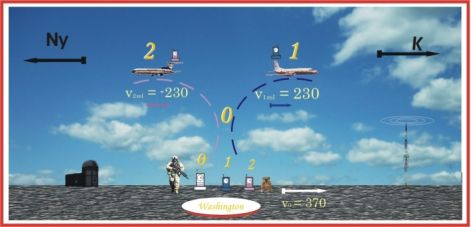
Legyen ebben a gondolatkísérletben is 370 m/s mind a keletnek, mind a  nyugatnak tartó repülőgép sebessége. Most végezzünk el egy olyan számítást, ami Washington szélességi körén (39 fok) történik. Így a földkerülés éppen 1 napig, azaz 86400 másodpercig   tart majd. A korábbi példákból ismert képleteket fogjuk használni. A keleti irányra vonatkozólag ez így fog szólni:

DT₁=-((v₀ + v_1rel )² - v₀² ) / 2c² * 86400 * 10⁹  [ns]

A konkrét számítások elvégzése után a keletnek tartó földkerülés időeltérése:

          DT₁= -168 [ns],

azaz a kék óra késik. A nyugatnak tartó földkerülés időeltérése:

                                DT₂ = +88 [ns],

 tehát a lila óra siet.

 Amint látjuk, e fiktív földkerülés számeredményei jellegükben (és véletlenül értékükben is)  jól közelítenek Hafele korábbi sejtéséhez:

Meg kell állapítanunk, hogy a reptetett atomórák a hétköznapi szemlélet számára igencsak extrém módon viselkednek. Sebesség hatására lassulnak, miközben rejtőző sebességek is beleszólnak a végeredménybe.  Valójában az órák járását a valódi sebesség határozza meg az abszolút 0 sebesség bázisán. 

   Hafele egy évig kereste az SR és GR labirintusában az atomóra-kísérletet leíró   képletet, és az elméleti indoklást.  A képlete  hibás, bár a konkrét esetben elég jól közelíti a helyes eredményt. Ez utóbbinak köszönheti, hogy a tudományos világ nagy megkönnyebbüléssel rögtön el is fogadta.  

   A súlyosabb hibát mégis a tudományos közösség követte el, amikor nem vizsgálta, elfogadta, sőt mindezideig nem korrigálta Hafele téveszméit. Hja, a fizikaprofesszorok okos emberek.  Nem kockáztatnak időt, energiát és renomét, hogy a GR és Hafele kacskaringóit követve végül felmutassanak egy másik bizonytalanságot, gyengítve ezzel a tudományba vetett hitet. Így azután a H-K kísérlet megmarad az áltudomány egyik szép példájának az un. mai tudomány kebelén belül.

Tassi Tamás

aparadox.hupont.hu